O是△ABC的外接圆，AB是直径，过BC的中点P作O的直径PG，与弦BC相交于点D，连接AG、CP、PB．（1）如图1，求证：AG=CP；（2）如图2，过点P作AB的垂线，垂足为点H，连接DH，求证：DH∥AG；（3）如

Question

O是△ABC的外接圆，AB是直径，过

BC

的中点P作 O的直径PG，与弦BC相交于点D，连接AG、CP、PB．
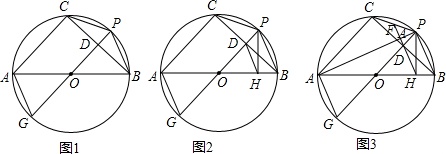
（1）如图1，求证：AG=CP；
（2）如图2，过点P作AB的垂线，垂足为点H，连接DH，求证：DH∥AG；
（3）如图3，连接PA，延长HD分别与PA、PC相交于点K、F，已知FK=2，△ODH的面积为2√(21)，求AC的长．

Answer 1

（1）证明：∵过

BC

的中点P作 O的直径PG，
∴CP=PB，
∵AB，PG是相交的直径，
∴AG=PB，
∴AG=CP；
（2）证明：如图 2，连接BG

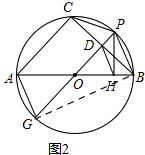
∵AB、PG都是 O的直径，
∴四边形AGBP是矩形，
∴AG∥PB，AG=PB，
∵P是弧BC的中点，
∴PC=BC=AG，
∴弧AG=弧CP，
∴∠APG=∠CAP，
∴AC∥PG，
∴PG⊥BC，
∵PH⊥AB，
∴∠BOD=90°=∠POH，
在△BOD和△POH中，

∠BOD=∠POH

∠BOD=∠BOD

OB=OP

，
∴△BOD≌△POH，
∴OD=OH，
∴∠ODH=(1)/(2)（180°-∠BOP）=∠OPB，
∴DH∥PB∥AG．
（3） 如图3，作CM⊥AP于M，ON⊥DH于N，

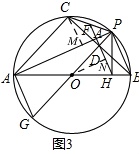
∴∠HON=(1)/(2)∠BOP=(1)/(2)∠COP=∠CAP，
∴△HON∽△CAM，
∴(OH)/(AC)=(HN)/(CM)，
作PQ⊥AC于Q，
∴四边形CDPQ是矩形，
△APH与△APQ关于AP对称，
∴HQ⊥AP，
由（1）有：HK⊥AP，
∴点K在HQ上，
∴CK=PK，
∴PK是△CMP的中位线，
∴CM=2FK=4，MF=PF，
∵CM⊥AP，HK⊥AP，
∴CM∥HK，
∴∠BCM+∠CDH=180°，
∵∠BCM=∠CAP=∠BAP=∠PHK=∠MHK，
∴∠MHK+∠CDH=180°，
∴四边形CDHM是平行四边形，
∴DH=CM=4，DN=HN=2，
∵S_△ODH=(1)/(2)DH×ON=(1)/(2)×4×ON=2√(21)，
∴ON=√(21)，
∴OH=√(HN2+ON2)=5，
∴AC=(OH×CM)/(HN)=10．