已知函数f（x）=lnx，g（x）=ex．（1）确定方程f（x）=x+1x-1实数根的个数；（2）我们把与两条曲线都相切的直线叫作这两条曲线的公切线，试确定曲线y=f（x），y=g（x）公切线的条数，并证明

Question

已知函数f（x）=lnx，g（x）=e^x．
（1）确定方程f（x）=(x+1)/(x-1)实数根的个数；
（2）我们把与两条曲线都相切的直线叫作这两条曲线的公切线，试确定曲线y=f（x），y=g（x）公切线的条数，并证明你的结论．

Answer 1

（1）由题意得lnx=(x+1)/(x-1)=1+(2)/(x-1)，即lnx-1=(2)/(x-1)．
分别作出y=lnx-1和y=(2)/(x-1)的函数图象，
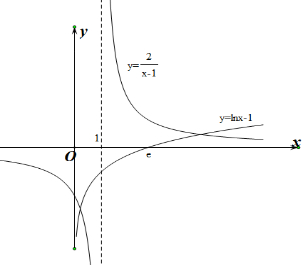由图象可知：y=lnx-1和y=(2)/(x-1)的函数图象有两个交点，
∴方程f（x）=(x+1)/(x-1)有两个实根；
（2） 曲线y=f（x），y=g（x）公切线的条数是2，证明如下：
设公切线与f（x）=lnx，g（x）=e^x的切点分别为（m，lnm），（n，eⁿ），m≠n，
∵f′（x）=(1)/(x)，g′（x）=e^x，
∴

(1)/(m)=en

(lnm-en)/(m-n)=(1)/(m)

，化简得（m-1）lnm=m+1，
当m=1时，（m-1）lnm=m+1不成立；
当m≠1时，（m-1）lnm=m+1化为lnm=(m+1)/(m-1)，
由（1）可知，方程lnm=(m+1)/(m-1)有两个实根，
∴曲线y=f（x），y=g（x）公切线的条数是2条．