已知椭圆C：x2a2+y2b2=1(a>b>0)的离心率为32，四个顶点构成的四边形的面积为4，过原点的直线l（斜率不为零）与椭圆C交于A，B两点，F1，F2为椭圆的左、右焦点，则四边形AF1BF2的周长为（

Question

已知椭圆C：

(x2)/(a2)+(y2)/(b2)=1(a>b>0)的离心率为(√(3))/(2)，四个顶点构成的四边形的面积为4，过原点的直线l（斜率不为零）与椭圆C交于A，B两点，F₁，F₂为椭圆的左、右焦点，则四边形AF₁BF₂的周长为（　　）

A. 4

B. 4

√(3)

C. 8

D. 8

√(3)

Answer 1

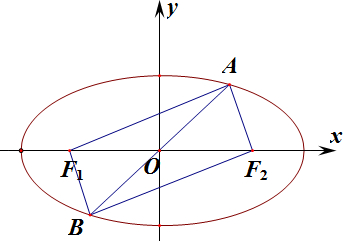由题意可知：椭圆C：(x2)/(a2)+(y2)/(b2)=1(a>b>0)焦点在x轴上，
由椭圆的离心率e=(c)/(a)=(√(3))/(2)，即4c²=3a²，
由四个顶点构成的四边形的面积为4，根据菱形的面积公式可知S=(1)/(2)×2a×2b=4，即ab=2，
由a²=c²+b²，解得：a=2，b=1，
则椭圆的标准方程为：(x2)/(4)+y2=1，
由椭圆的定义可知：四边形AF₁BF₂的周长4a=8，
故选C．