早教吧作业答案频道 -->数学-->
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH(1)求证:平面AGH⊥平面EFG(2)若a=4,求三棱锥G-ADE的体积.
题目详情
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH
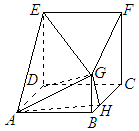
(1)求证:平面AGH⊥平面EFG
(2)若a=4,求三棱锥G-ADE的体积.

(1)求证:平面AGH⊥平面EFG
(2)若a=4,求三棱锥G-ADE的体积.
▼优质解答
答案和解析
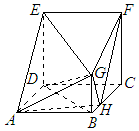 证明:(1)连接FH,
证明:(1)连接FH,
∵CD⊥BC,CD⊥CF,
∴CD⊥平面BCFG. 又∵GH⊂平面BCFG,
∴CD⊥GH. 又∵EF∥CD,
∴EF⊥GH,
∵AB=2BG=4BH=a,
∴GH=
=
,FH=
=
,GF=
=
,
∴FH2=FG2+GH2,
∴GH⊥FG.
又∵EF∩FG=F,EF⊂平面EFG,FG⊂平面EFG,
∴GH⊥平面EFG.又GH⊂平面AGH,
∴平面AGH⊥平面EFG.
(2)∵CF⊥平面ABCD,BG⊥平面ABCD,
∴CF∥BG,又∵ED∥CF,
∴BG∥ED,又BG⊄平面ADE,DE⊂平面ADE,
∴BG∥平面ADE,
∴VG-ADE=VB-ADE=VE-ABD=VF-ABD=
S△ABD•CF=
×
×42×4=
.
 证明:(1)连接FH,
证明:(1)连接FH,∵CD⊥BC,CD⊥CF,
∴CD⊥平面BCFG. 又∵GH⊂平面BCFG,
∴CD⊥GH. 又∵EF∥CD,
∴EF⊥GH,
∵AB=2BG=4BH=a,
∴GH=
| BG2+BH2 |
| ||
| 4 |
| FC2+HC2 |
| 5a |
| 4 |
a2+
|
| ||
| 2 |
∴FH2=FG2+GH2,
∴GH⊥FG.
又∵EF∩FG=F,EF⊂平面EFG,FG⊂平面EFG,
∴GH⊥平面EFG.又GH⊂平面AGH,
∴平面AGH⊥平面EFG.
(2)∵CF⊥平面ABCD,BG⊥平面ABCD,
∴CF∥BG,又∵ED∥CF,
∴BG∥ED,又BG⊄平面ADE,DE⊂平面ADE,
∴BG∥平面ADE,
∴VG-ADE=VB-ADE=VE-ABD=VF-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 32 |
| 3 |
看了 在多面体ABCDEFG中,四...的网友还看了以下:
已知a+b=c,a-b=d,c,d为非零向量,求证:|a|=|b|<=>c⊥d 一定要解释其几何意 2020-04-05 …
已知a+b=c,a-b=d,c,d为非零向量,求证:|a|=|b|c⊥d的几何意义 2020-04-05 …
现有A,B,C,D四种物质,已知A,B为黑色粉末,C,D为无色气体,A,B在高温下作用能生成D,A 2020-05-17 …
一道初二几何题不会做,请会的人教我一下!已知:点A’、B’、C’、D’分别在正方形的边AB、BC、 2020-06-05 …
一次函数y=1/3+1的图像与x轴,y轴分别交与A,B,点C的坐标为(2,0)(1)求直线BC的函 2020-06-14 …
蓄水池有A,C两个进水管和B,D两个出水管.要注满一池水,单开A管需要30分钟,单开C管需要50分 2020-06-23 …
1.设abcd是四个整数,且使m=(ab+cd)^2-1/4(a^2+b^2-c^2-d^2)^2 2020-07-09 …
下图为某地区港口分布示意图。完成题。1.导致a港口解冻日期比其他港口晚的主要因素是2.b.c.d三港 2020-11-04 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
如果有A、B、C、D、E、F六种生物,其中A、C同属不同种,B、C同科不同属,C、D同目不同科,B、 2020-12-21 …