早教吧作业答案频道 -->数学-->
如图,二次函数y=-ax2+2ax+c(a>0)的图象交x轴于A,B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF.(1)求A点坐
题目详情
如图,二次函数y=-ax2+2ax+c(a>0)的图象交x轴于A,B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF.
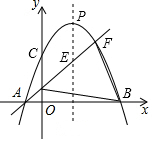
(1)求A点坐标;
(2)若△BDF的面积为12,求此二次函数的表达式;
(3)设二次函数图象顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此二次函数的表达式.

(1)求A点坐标;
(2)若△BDF的面积为12,求此二次函数的表达式;
(3)设二次函数图象顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此二次函数的表达式.
▼优质解答
答案和解析
(1)当y=0时,kx+2k=0,解得x=-2,则A(-2,0);
(2)∵二次函数y=-ax2+2ax+c(a>0)的图象的对称轴为直线x=-
=1,
∴B点坐标为(4,0),
把A(-2,0)代入y=-ax2+2ax+c得-4a-4a+c=0,
∴c=8a,
∴抛物线解析式为y=-ax2+2ax+8a,
∵DE=EF,
∴F点的横坐标为2,
∴F(2,8a),
把F(2,8a)代入y=kx+2k得8a=2k+2k,解得k=2a,
∴y=2ax+4a,
当x=0时,y=4a,则D(0,4a),
∵S△BDF=S△FAB-S△DAB,
∴
•(4+2)•8a-
•(4+2)•4a=12,解得a=1,
∴抛物线解析式为y=-x2+2x+8;
(3)抛物线的解析式表示为y=-ax2+2ax+8a,D(0,4a),F(2,8a),
当x=0时,y=-ax2+2ax+8a=8a,则C(0,8a),
当x=1时,y=-ax2+2ax+8a=9a,则P(1,9a),
∵F(2,8a),C(0,8a),
∴CF∥x轴,E(1,8a),
∴△PCF为等腰三角形,
∴PE平分∠CPF,即∠CPF=2∠CPE,
∵∠CPF=2∠DAB,
∴∠DAB=∠CPE,
∴Rt△ADO∽Rt△PCE,
∴
=
,即
=
,解得a=
或a=-
(舍去),
∴抛物线的解析式表示为y=-
x2+
x+4
.
(2)∵二次函数y=-ax2+2ax+c(a>0)的图象的对称轴为直线x=-
| 2a |
| 2×(-a) |
∴B点坐标为(4,0),
把A(-2,0)代入y=-ax2+2ax+c得-4a-4a+c=0,
∴c=8a,

∴抛物线解析式为y=-ax2+2ax+8a,
∵DE=EF,
∴F点的横坐标为2,
∴F(2,8a),
把F(2,8a)代入y=kx+2k得8a=2k+2k,解得k=2a,
∴y=2ax+4a,
当x=0时,y=4a,则D(0,4a),
∵S△BDF=S△FAB-S△DAB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴抛物线解析式为y=-x2+2x+8;
(3)抛物线的解析式表示为y=-ax2+2ax+8a,D(0,4a),F(2,8a),
当x=0时,y=-ax2+2ax+8a=8a,则C(0,8a),
当x=1时,y=-ax2+2ax+8a=9a,则P(1,9a),
∵F(2,8a),C(0,8a),
∴CF∥x轴,E(1,8a),
∴△PCF为等腰三角形,
∴PE平分∠CPF,即∠CPF=2∠CPE,
∵∠CPF=2∠DAB,
∴∠DAB=∠CPE,
∴Rt△ADO∽Rt△PCE,
∴
| AO |
| PE |
| OD |
| CE |
| 2 |
| a |
| 4a |
| 1 |
| ||
| 2 |
| ||
| 2 |
∴抛物线的解析式表示为y=-
| ||
| 2 |
| 2 |
| 2 |
看了 如图,二次函数y=-ax2+...的网友还看了以下:
求几条基本初等函数的题1、设关于x的函数f(x)=4^x—2^x+1—b(b属于R),若函数有零点 2020-04-27 …
A={(x,y)\x,y属于R},B=R,对任何的(x,y)属于A,(x,y)为什么不是从集合A到 2020-05-20 …
如图,已知反比例函数y=k/x(x>0)的图像与一次函数y=kx+b的图像交于点(2,1),直线y 2020-05-21 …
如何解答初三的反比例函数与一次函数如图,一次函数Y=KX+b的图像与反比例函数Y=X|M的图像交于 2020-05-21 …
初二函数已知一次函数y=x与y=-x+8若函数y=-x+8的图象交y轴于点A,交函数y=x于点B求 2020-06-14 …
已知反比例函数y=k/x与一次函数y=2x-1的图像交于点A(a,b),且一次函数y=2x-1经过 2020-06-14 …
(2013•滨湖区二模)如图,已知二次函数y=ax2+bx+c的图象交x轴的负半轴于点A(-5,0 2020-07-20 …
对数函数关于各直线对称的关系式请说明对数函数关于Y轴,X轴,原点,Y=X,Y=-X对称的关系式!如 2020-07-30 …
已知一次函数y=kx+b的图象交y轴于点A(0,1),交x轴于点C,且与正比例函数y=12x的图象相 2020-11-01 …
如图,已知a(-4,2分之1),b(-1,2)是一次函数y=kx+b与反比例函数y=,AC⊥x轴于C 2020-12-08 …