已知f（x）=（x2-3）ex（其中x∈R，e是自然对数的底数），当t1>0时，关于x的方程[f（x）-t1][f（x）-t2]=0恰好有5个实数根，则实数t2的取值范围是（）A.（-2e，0）B.（-2e，0]C.[-2e，6e-3]D.

Question

已知f（x）=（x²-3）e^x（其中x∈R，e是自然对数的底数），当t₁>0时，关于x的方程[f（x）-t₁][f（x）-t₂]=0恰好有5个实数根，则实数t₂的取值范围是（　　）

A. （-2e，0）

B. （-2e，0]

C. [-2e，6e^-3]

D. （-2e，6e^-3）

Answer 1

f（x）=（x²-3）e^x的导数为
f′（x）=（x²+2x-3）e^x=（x-1）（x+3）e^x，
当-3当x>1或x<-3时，f′（x）>0，f（x）递增．
可得f（x）的极小值为f（1）=-2e，极大值为f（-3）=6e^-3，
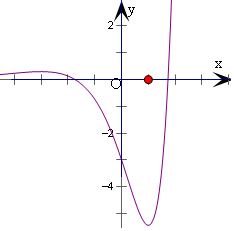
作出y=f（x）的图象，如图：
当t₁>0时，关于x的方程[f（x）-t₁][f（x）-t₂]=0
恰好有5个实数根，
即为f（x）=t₁或f（x）=t₂恰好有5个实数根，
若t₁>6e^-3，f（x）=t₁只有一个实根，不合题意；
若01<6e^-3，f（x）=t₁有三个实根，只要-2e2≤0，满足题意；
若t₁=6e^-3，f（x）=t₁有两个实根，只要02<6e^-3，满足题意；
综上可得，t₂的范围是（-2e，6e^-3）．
故选：D．