早教吧作业答案频道 -->数学-->
完成下列推理说明:(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:因为∠1=∠2(已知),且∠1=∠4()所以∠2=∠4(等量代换)所以CE∥BF()所以∠=∠3()又因为
题目详情
完成下列推理说明:
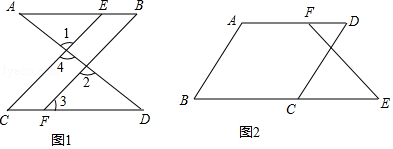
(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
因为∠1=∠2(已知),且∠1=∠4(___)
所以∠2=∠4(等量代换)
所以CE∥BF(___)
所以∠___=∠3(___)
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD(___)
(2)如图2,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (___)
∴∠B=___(___)
又∵∠B=∠D( 已知 ),
∴∠___=∠___ (等量代换)
∴AD∥BE(___)
∴∠E=∠DFE(___)
(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
因为∠1=∠2(已知),且∠1=∠4(___)
所以∠2=∠4(等量代换)
所以CE∥BF(___)
所以∠___=∠3(___)
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD(___)
(2)如图2,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (___)
∴∠B=___(___)
又∵∠B=∠D( 已知 ),
∴∠___=∠___ (等量代换)
∴AD∥BE(___)
∴∠E=∠DFE(___)

▼优质解答
答案和解析
 (1)理由:
(1)理由:
因为∠1=∠2(已知),且∠1=∠4(对顶角相等),
所以∠2=∠4(等量代换),
所以CE∥BF(同位角相等,两直线平行),
所以∠C=∠3(两直线平行,同位角相等),
又因为∠B=∠C(已知),
所以∠3=∠B(等量代换),
所以AB∥CD(内错角相等,两直线平行);
故答案为:对顶角相等,同位角相等,两直线平行,C,两直线平行,同位角相等,内错角相等,两直线平行;
(2)证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD (同旁内角互补,两直线平行),
∴∠B=∠DCE(两直线平行,同位角相等),
又∵∠B=∠D(已知),
∴∠DCE=∠D (等量代换),
∴AD∥BE(内错角相等,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行,∠DCE,两直线平行,同位角相等,DCE,D,内错角相等,两直线平行,两直线平行,内错角相等.
 (1)理由:
(1)理由:因为∠1=∠2(已知),且∠1=∠4(对顶角相等),
所以∠2=∠4(等量代换),
所以CE∥BF(同位角相等,两直线平行),
所以∠C=∠3(两直线平行,同位角相等),
又因为∠B=∠C(已知),
所以∠3=∠B(等量代换),
所以AB∥CD(内错角相等,两直线平行);
故答案为:对顶角相等,同位角相等,两直线平行,C,两直线平行,同位角相等,内错角相等,两直线平行;
(2)证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD (同旁内角互补,两直线平行),
∴∠B=∠DCE(两直线平行,同位角相等),
又∵∠B=∠D(已知),
∴∠DCE=∠D (等量代换),
∴AD∥BE(内错角相等,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行,∠DCE,两直线平行,同位角相等,DCE,D,内错角相等,两直线平行,两直线平行,内错角相等.
看了 完成下列推理说明:(1)如图...的网友还看了以下:
已知向量a=(2,1),b=(x,y).(1)若x∈{-1,0,1,2},y∈{-1,0,1},求向 2020-03-30 …
求一数列.高2.a(n+1)=2an/2an+1已知a1=1a(n+1)=2an/2an+1求数列 2020-04-25 …
S=(1+1/1*2+(2+1/2*3)+(3+1/3*4)+...+(20+1/20*21)S= 2020-04-27 …
几道数学计算题(请写过程)第一题1/2+(1/3+2/3)+(1/4+2/4+3/4)+…+(1/ 2020-05-16 …
设函数(x)=ax^2lnx+b(x-1)(x>0),曲线y=f(x)过点(e,e^2-e+1)且 2020-07-15 …
(1)已知a+b=-c,则a(1/a+1/b)+b(1/a+1/c)+c(1/a+1/b)的值是多少 2020-10-31 …
已知数列{a底n}中,a1=a2=1,且an=an-1+an-2(n≥3,n∈n*),设bn=an/ 2020-11-27 …
计算一道数学题,(1+1/2)×(1+1/3)×(1+1/4)×(1+1/5)×(1+1/6)×(1 2020-11-30 …
1.已知1/x+1/y=1/x+y,求y/x+x/y2.已知非零实数abc满足a^+b^+c^=1, 2020-12-07 …
关于必要不充分条件的疑问设a,b是方程x^2-mx+n=0的两个实根,那么"m>1且n>1"是"两根 2020-12-31 …