早教吧作业答案频道 -->数学-->
已知:如图,在△ABC中,∠ACB=90°,AE是∠BAC的角平分线,CD是高,AE与CD相交于点F.(1)若AC=8,BC=6,AB=10,求AB上的高CD.(2)求证:∠CEF=∠CFE.
题目详情
已知:如图,在△ABC中,∠ACB=90°,AE是∠BAC的角平分线,CD是高,AE与CD相交于点F.
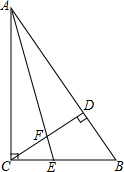
(1)若AC=8,BC=6,AB=10,求AB上的高CD.
(2)求证:∠CEF=∠CFE.

(1)若AC=8,BC=6,AB=10,求AB上的高CD.
(2)求证:∠CEF=∠CFE.
▼优质解答
答案和解析
(1) CD=
AC•BC÷
÷AB
=8×6÷10
=4.8.
故AB上的高CD是4.8.
(2)证明:∵∠CAD+∠ACD=∠CAD+∠B=90°,
∴∠ACD=∠B,
∵AE是∠BAC的角平分线,
∴∠FAC=∠BAF,
∴∠ACD+∠FAC=∠BAF+∠B,
∴∠CEF=∠CFE.
| 1 |
| 2 |
| 1 |
| 2 |
=8×6÷10
=4.8.
故AB上的高CD是4.8.
(2)证明:∵∠CAD+∠ACD=∠CAD+∠B=90°,
∴∠ACD=∠B,
∵AE是∠BAC的角平分线,
∴∠FAC=∠BAF,
∴∠ACD+∠FAC=∠BAF+∠B,
∴∠CEF=∠CFE.
看了 已知:如图,在△ABC中,∠...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
数集A满足:若a属于A,a≠1,则1-a分之一属于A.证明:集合A中至少有三个不同的元素 要证明 2020-04-05 …
如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的 2020-05-15 …
设函数f(x)=x^2-alnx与g(x)=(1/a)x-√x的图像分别交直线x=1于点A、B,且 2020-05-15 …
如图,在直角坐标系中,抛物线y=ax^2+bx+c(a不等于0)与x轴交于点A(-1,0),B(3 2020-05-16 …
如图,在直角坐标系中,M为x轴上一点,⊙M交x轴于A、B两点,交y轴于C、D两点,P为BC上的一个 2020-06-14 …
已知直线AB与抛物线y^2=2px(p大于0)交于A,B两点,且以AB为直径的圆经过坐标原点O,O 2020-06-14 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
设集合A={x|x^2-4x=0},B={x|ax^2-2x+8=0},若A交B=B,求实数a的取 2020-07-09 …
已知抛物线y=1/4x平方+1的顶点为M直线L过F(0,2)且与抛物线分别交于A,B两点,过AB分 2020-07-22 …