将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(4,0),点B(0,3),点O(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′
将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(4,0),点B(0,3),点O(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′.
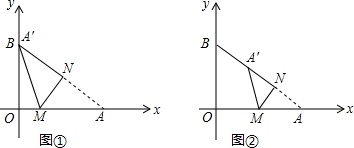
(1)如图①,当点A′与顶点B重合时,求点M的坐标;
(2)如图②,当动点M运动到边AO的中点时,求点O与点A′的距离.
答案和解析
(1)∵点A(4,0),点B(0,3),
∴OA=4,OB=3,
∴AB=
=5,
由折叠的性质得:AN=BN=AB=2.5,∠ANM=90°=∠AOB,
∵∠NAM=∠OAB,
∴△AMN∽△ABO,
∴=,
即=,
解得:AM=,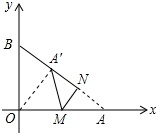
∴OM=OA-AM=4-=,
∴M(,0);
(2)连接OA′,如图所示:
∵M是AO的中点,
∴AM=OM=2,
由(1)得:△AMN∽△ABO,
∴=,即=,
解得:AN=,
由折叠的性质得:A′N=AN=,
∴A′A=,MN是△OAA′的中位线,
∴MN∥OA′,∠AA′O=∠ANM=90°,
∴OA′===.
某同学将直角梯形纸片ABCD的一直角沿折痕AE折叠,顶点D恰好落在腰的中点M处某同学将直角梯形纸片 2020-04-27 …
如图 已知 直线l∶y=-√3x÷3+√3交x轴于点A 交y轴于点B 将△AOB沿直线l翻折 点如 2020-05-16 …
急!某同学将直角梯形纸片ABCD的一直角沿折痕AE折叠,顶点D恰好落在腰的中点M处,某同学将直角梯 2020-05-19 …
如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△ 2020-06-15 …
将△EFP沿直线l向左到图2的位置时2)将△EFP沿直线向左平移到图2的位置时,EP交AC于点Q, 2020-06-22 …
将直线y=2x+3沿着y轴平移后经过点(2,-1)求:(1)直线平移后的表达式;(2)直线平移将直 2020-07-29 …
如图1,角ABC=90°,AB=2,点D为BC边上的一个动点,连接AD,将三角形ABD沿AD,角AB 2020-11-03 …
如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△C 2020-11-03 …
如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折, 2020-11-03 …
如图,点P是正方形ABCD内一点,PA=1,PB=22,PD=10,将△ADP沿点A旋转至△ABP′ 2020-11-04 …



