早教吧作业答案频道 -->数学-->
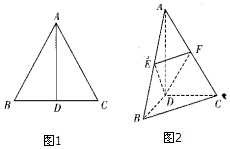
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.(1)求证:BC∥平面DEF;(2)求多面体D-BCEF的体积.
题目详情
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
(1)求证:BC∥平面DEF;
(2)求多面体D-BCEF的体积.

(1)求证:BC∥平面DEF;
(2)求多面体D-BCEF的体积.
▼优质解答
答案和解析
证明:(1)因为点E,F分别是AB,AC的中点,所以EF∥BC.
又因为BC⊄平面DEF,EF⊂平面DEF,
所以BC∥平面DEF. …(5分)
(2)依题意,AD⊥BD,AD⊥CD,且BD∩DC=D,
所以AD⊥平面BCD,
又因为二面角B-AD-C为直二面角,所以BD⊥CD,
所以V三棱锥A-BCD=
S△BCD•AD=
×
×1×1×
=
,
V三棱锥F-ADE=
S△ADE•
CD=
×
×
×
×
×1=
,
所以VD-BCFE=V三棱锥A-BCD-V三棱锥F-ADE=
-
=
. …(12分)
又因为BC⊄平面DEF,EF⊂平面DEF,
所以BC∥平面DEF. …(5分)
(2)依题意,AD⊥BD,AD⊥CD,且BD∩DC=D,
所以AD⊥平面BCD,
又因为二面角B-AD-C为直二面角,所以BD⊥CD,
所以V三棱锥A-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 6 |
V三棱锥F-ADE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 24 |
所以VD-BCFE=V三棱锥A-BCD-V三棱锥F-ADE=
| ||
| 6 |
| ||
| 24 |
| ||
| 8 |
看了 如图,边长为2的等边三角形A...的网友还看了以下:
求面积三角形的面积为()平方分米.平行四边形的一条底长为10分米,这条底三角形的面积为()平方分米 2020-05-14 …
在正方体ABCDA`B`C`D`中,O为底面ABCD是中点,P是DD`的中点,设Q是CC`上的点, 2020-05-16 …
求∫∫∫(D)1/(1+x+y+z)^3,其中D为平面x+y+z=1与三个左边面所围成的四面体∫( 2020-05-16 …
设z为任意实数,则相应的所有点P(1,2,z)的集合确定的图形为A.直线B.圆C.平面D.半平面 2020-05-17 …
a=d^2*s/(d*t^2)为什么上面d有平方而下面没有 2020-06-12 …
(2014•海淀区二模)在△ABC中,∠ABC=90°,D为平面内一动点,AD=a,AC=b,其中 2020-06-15 …
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=3,PD⊥底面ABC 2020-07-31 …
如图,在四棱锥D′-ABCE中,底面为直角梯形,AB=2BC=2CE=2,且AB⊥BC,AB∥CE 2020-07-31 …
一条直线与两条平行线中的一条成为异面直线,则它与另一条()A.相交B.异面C.相交或异面D.平行 2020-08-02 …
过一条直线和这条直线外不共线的三点,可确定个平面.四条直线过同一点,过每两条直线做一个平面,可以作个 2020-11-03 …