早教吧作业答案频道 -->数学-->
已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=3,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).(1)证明:平面DEG∥平面ABF;(2)求
题目详情
已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=
,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).
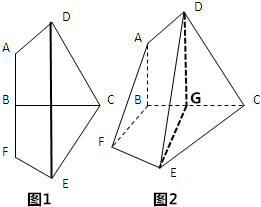
(1)证明:平面DEG∥平面ABF;
(2)求多面体ABC-DEF的体积.
| 3 |

(1)证明:平面DEG∥平面ABF;
(2)求多面体ABC-DEF的体积.
▼优质解答
答案和解析
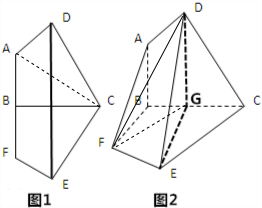 (1)证明:由平面图形,可得DG∥AB,GE∥BF,
(1)证明:由平面图形,可得DG∥AB,GE∥BF,
∵DG⊄平面ABF,AB⊂平面ABF,
∴DG∥平面ABF.
同理GE∥平面ABF.
∵DG∩GE=G,
∴平面DEG∥平面ABF;
(2) 图(1),连接AC,则由勾股定理可得AC=2,
∴∠BCD=60°,
∴DG=
,BG=
.
图(2),连接DF,GF,则多面体ABC-DEF的体积=VF-ABGD+VF-DGE=
×
×
×1+
×
×
×
=
.
 (1)证明:由平面图形,可得DG∥AB,GE∥BF,
(1)证明:由平面图形,可得DG∥AB,GE∥BF,∵DG⊄平面ABF,AB⊂平面ABF,
∴DG∥平面ABF.
同理GE∥平面ABF.
∵DG∩GE=G,
∴平面DEG∥平面ABF;
(2) 图(1),连接AC,则由勾股定理可得AC=2,
∴∠BCD=60°,
∴DG=
| 3 |
| 2 |
| ||
| 2 |
图(2),连接DF,GF,则多面体ABC-DEF的体积=VF-ABGD+VF-DGE=
| 1 |
| 3 |
1+
| ||
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
7
| ||
| 12 |
看了 已知平面五边形ADCEF关于...的网友还看了以下:
(1)把两个含有45°角的直角三角板如图1放置,点D在BC上,连接BE,AD,AD的延长线交BE于 2020-04-06 …
三角形ABC中,E为AB中点,以E为圆心.EB为半径画弧.叫BC于D,连接ED,延长ED到F,使D 2020-05-17 …
三角形ABC中AB=AC,G是△ABC重心,连AG并延长交BC于D,连BG并延长交AC于E,AD= 2020-06-06 …
三角形ABC的面积为1.E是AC中点,O是BE中点,连结AO,并延长交BC于D,连结CO并延长交A 2020-06-06 …
图中所示为用三角形刚性细杆AB、BC、CD连成的平面连杆结构图.AB和CD杆可分别绕过A、D的垂直 2020-06-15 …
O是三角形ABC外接圆的圆心连接AO交BC于D连接BO交AC于E连接CO交AB于F,R为半径,求证 2020-06-27 …
如图所示,直线EF‖GH,A是直线EF上一点,B,C,D分别是直线GH上的三点,且AB=AC,D 2020-07-09 …
如图,在△ABC中,点D、E分别在BC,AB上,连接AD,CE交于点F,点G在CE上,且DG‖AB 2020-08-02 …
如图1,对△ABC,D是BC边上一点,连结AD,当AB2AC2=BDCD时,称AD为BC边上的“平方 2020-11-08 …
关于三角形内任意一点的问题一个三角形内任意一点P,连接AP并延长交BC于D,连接BP并延长交AC于E 2020-12-25 …