早教吧作业答案频道 -->数学-->
选修4-4:坐标系与参数方程已知直线l的参数方程为(t为参数),曲线C的参数方程为(θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).求:(1)线段AB的中点坐
题目详情
选修4-4:坐标系与参数方程
已知直线l的参数方程为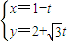 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为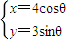 (θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).
(θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).
求:(1)线段AB的中点坐标;
(2)线段AB的长;
(3)|PA-PB|的值.
已知直线l的参数方程为
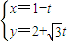 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为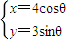 (θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).
(θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).求:(1)线段AB的中点坐标;
(2)线段AB的长;
(3)|PA-PB|的值.
▼优质解答
答案和解析
【答案】分析:先将直线的参数方程化为(l为参数)的形式,此时,|l|的几何意义为(a,b)点到(x,y)的距离,(1)设点A对应的参数为l1,点B对应的参数为l2,将直线的参数方程代入曲线,利用韦达定理即可得l1+l2,而即为AB中点对应的参数,代入参数方程可得中点坐标;(2)AB的长度即为AB参数差的绝对值,利用韦达定理代入求值即可;因为点P(1,2)在直线上,且点P在椭圆内,故A、B两点分布在点P两侧,即l1与l2异号,所以|PA-PB|的值即为l1+l2的绝对值,代入求值即可由题意可知,直线l的斜率为-,倾斜角为∴直线l的参数方程可改写为(l为参数,|l|的几何意义为(1,2)点到(x,y)的距离),曲线C的普通方程为,将直线方程代入曲线C的方程可得,,设点A对应的参数为l1,点B对应的参数为l2,∵△>0,∴,,由参数l的几何意义得(1)中点对应的参数为,代入直线参数方程得∴线段AB中点坐标为;(2)弦AB的长为AB=|l1-l2|===;(3)∵点P(1,2)在直线上,且点P在椭圆内,故A、B两点分布在点P两侧,即l1与l2异号∴.点评:本题考查了直线的参数方程,参数的几何意义及其应用,椭圆的参数方程及其与一般方程的互化,韦达定理在解决解析几何问题中的重要应用
看了 选修4-4:坐标系与参数方程...的网友还看了以下:
在校秋季运动会上,九(1)班男生参加4×100m接力赛中出现了接力棒掉棒现象,痛失了取得优异成绩的 2020-05-17 …
运动会开赛在即,AB两班各组织了4名选手参加4×50米接力赛,通过打探,B班知道A班参赛的4名选手 2020-05-17 …
一道参数题目已知设直线l:x=4+t*cos(a),y=-2+t*sin(a)(t为参数,a为倾斜 2020-06-13 …
X轴交点是4.8,Y轴交点是—5.76,写出一个2次方程如题.结果要写成Y=ax^2+bx+c如果 2020-07-20 …
若方程x方+px+4=0的解集为A,方程x方+x+q=0的解集为B,且A和B的交集为4,求p和q 2020-07-30 …
关于参数方程的简单问题已知经过点P(2,0),斜率为4/3的直线和抛物线y^2=2x相交于A,B两 2020-07-30 …
已知直线C1x=1+tcosαy=tsinα(t为参数),C2x=cosθy=sinθ(θ为参数) 2020-07-31 …
已知曲线C的参数方程为x=3+3cosθy=3sinθ(θ是参数),以原点O为极点,以x轴正半轴为 2020-07-31 …
1.设直线L经过M.(1,5)倾斜角为π/3(1)求直线L的参数方程(2)求直线L和直线x—y-2 2020-08-01 …
求点拔一数学题(参数方程)经过点P(2,0),斜率为4/3的直线和抛物线y^2=2x相交与A,B两点 2021-01-22 …