已知椭圆C1与双曲线C2具有相同的焦点F1，F2，A为C1与C2的一个公共点，△AF1F2为等腰三角形，设椭圆C1与双曲线C2的离心率分别为e1，e2，则（）A.e1e2=1B.e1e2=2C.e1+e2=2D.1e1+1e2=2

Question

已知椭圆C₁与双曲线C₂具有相同的焦点F₁，F₂，A为C₁与C₂的一个公共点，△AF₁F₂为等腰三角形，设椭圆C₁与双曲线C₂的离心率分别为e₁，e₂，则（　　）

A. e₁e₂=1

B. e₁e₂=2

C. e₁+e₂=2

D.

(1)/(e1)+(1)/(e2)=2

Answer 1

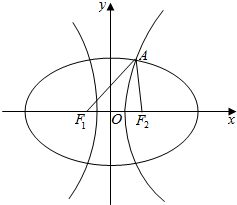由题意画出图象：
设椭圆与双曲线的标准方程分别为：(x2)/(a12)+(y2)/(b12)=1和(x2)/(a22)-(y2)/(b22)=1，
（a₁，a₂，b₁，b₂>0，a₁>b₁），
由图可得，|AF₁|>|AF₂|，
因为△AF₁F₂的等腰三角形，所以由图可得|AF₁|=|F₁F₂|=2c，
由椭圆、双曲线的定义得：|AF₁|+|AF₂|=2a₁，|AF₁|-|AF₂|=2a₂，
两式相加得：2|AF₁|=2a₁+2a₂=4c，
即a₁+a₂=2c，两边同除以c得：(a1)/(c)+(a2)/(c)=2，
则(1)/((c)/(a1))+(1)/((c)/(a2))=2，所以(1)/(e1)+(1)/(e2)=2，
故选：D．