早教吧作业答案频道 -->物理-->
在真空中的xOy平面内,有一磁感强度大小为B、方向垂直于纸面向里的匀强磁场.过原点O的直线MN是磁场的边界,其斜率为k.在坐标原点O处有一电子源,能在xOy平面内朝某一方向向磁场发射
题目详情
在真空中的xOy平面内,有一磁感强度大小为B、方向垂直于纸面向里的匀强磁场.过原点O的直线MN是磁场的边界,其斜率为k.在坐标原点O处有一电子源,能在xOy平面内朝某一方向向磁场发射不同速率的电子,电子的质量为m、电荷量为q,电子重力不计.
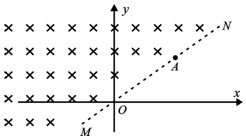
(1)若某一电子从MN上的A点离开磁场时的速度方向平行于x轴,AO的距离为L,求电子射入磁场时的速率;
(2)若在直线MN的右侧加一水平向右的匀强电场(图中未画出),电场强度大小为E;保持电子源向磁场发射电子的速度方向不变,调节电子源,使射入磁场的电子速率在0和足够大之间均有分布.请画出所有电子第一次到达MN右侧最远位置所组成的图线;并通过计算求出任一电子第一次到达MN右侧最远位置的横坐标x和纵坐标y的关系式.

(1)若某一电子从MN上的A点离开磁场时的速度方向平行于x轴,AO的距离为L,求电子射入磁场时的速率;
(2)若在直线MN的右侧加一水平向右的匀强电场(图中未画出),电场强度大小为E;保持电子源向磁场发射电子的速度方向不变,调节电子源,使射入磁场的电子速率在0和足够大之间均有分布.请画出所有电子第一次到达MN右侧最远位置所组成的图线;并通过计算求出任一电子第一次到达MN右侧最远位置的横坐标x和纵坐标y的关系式.
▼优质解答
答案和解析
(1)设直线MN与x轴正方向的夹角为θ,则k=tanθ,sinθ=
…①
设从A点离开磁场的电子在磁场中运动的半径为r,由几何关系得r=
…②
电子射入磁场时的速率为v,根据牛顿第二定律qvB=m
…③
联立①②③得v=
…④
(2)曲线如图所示
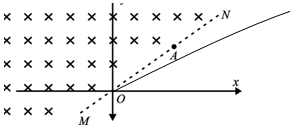
所有电子从MN上的点离开磁场时速度方向都平行于x轴,电子进入电场作匀减速直线运动,设曲线上的点P(x,y)
电子匀减速直线运动的加速度为a=
…⑤
根据运动学公式得v2=2a(x-
)…⑥
根据几何关系得(
)2+(r-y)2=r2…⑦
qvB=m
…⑧
联立⑤⑥⑦⑧解得x=
+
(其中k′=
)
答:
(1)电子射入磁场时的速率为v=
(2)图线见解析,横坐标x和纵坐标y的关系式为x=
+
(其中k′=
)
| k | ||
|
设从A点离开磁场的电子在磁场中运动的半径为r,由几何关系得r=
| L |
| 2sinθ |
电子射入磁场时的速率为v,根据牛顿第二定律qvB=m
| v2 |
| r |
联立①②③得v=
qBL
| ||
| 2mk |
(2)曲线如图所示

所有电子从MN上的点离开磁场时速度方向都平行于x轴,电子进入电场作匀减速直线运动,设曲线上的点P(x,y)
电子匀减速直线运动的加速度为a=
| qE |
| m |
根据运动学公式得v2=2a(x-
| y |
| k |
根据几何关系得(
| y |
| k |
qvB=m
| v2 |
| r |
联立⑤⑥⑦⑧解得x=
| y2 |
| k′ |
| y |
| k |
| 8k4mE |
| (1+k2)2qB2 |
答:
(1)电子射入磁场时的速率为v=
qBL
| ||
| 2mk |
(2)图线见解析,横坐标x和纵坐标y的关系式为x=
| y2 |
| k′ |
| y |
| k |
| 8k4mE |
| (1+k2)2qB2 |
看了 在真空中的xOy平面内,有一...的网友还看了以下:
相吸的磁铁为什么会加大磁场?相吸的磁铁为什么会加大磁场.两个磁铁N极与S极互相吸形成一个大的方形磁铁 2020-03-30 …
自由转动小磁针静止时沿竖直方向,且S极向下,为什么小磁针此时的位置在地球的北磁极附近?若在北磁极, 2020-04-26 …
关于磁通量,正确的说法有()A.磁通量不仅有大小而且有方向,是矢量B.磁通量大,磁感应强度不一定大 2020-05-16 …
和小磁针看到这么一句话:在地理北极,指南针的N极指向地磁北极.在地磁北极,指南针的N极垂直于地面指 2020-06-07 …
如图所示,M、N和P是以MN为直径的半圆弧上的三点,O为半圆弧的圆心,∠MOP=60°,在M、N处 2020-07-29 …
设f(N)、g(N)是定义在正数集上的正函数.如果存在正的常数C和自然数N0,使得当N≥N0时有f 2020-07-31 …
如图(a)所示,真空中半径为R的圆形区域内存在匀强磁场,磁场方向垂直纸面向外,磁场右侧有一对平行金 2020-08-02 …
如图所示,在NOQ范围内有垂直于纸面向里的匀强磁场I,在MOQ范围内有垂直于纸面向外的匀强磁场Ⅱ, 2020-08-02 …
下列关于磁感线的描述正确的是()A.磁感线是存在于磁体外部的曲线B.磁感线是起始于磁体的N极终止于S 2020-11-01 …
在如图所示的虚线MN上方存在着磁感应强度为B的匀强磁场,磁场方向垂直纸面向外,纸面上直角三角形OPQ 2020-12-20 …