在如图所示的四棱锥A—BCDE中AD⊥底面BCDEAC⊥BCAE⊥BE.(1)求证:A、B、C、D、E五点都在以AB为直径的同一球面上.(2)若∠CBE=90°CE=AD=1求B、D两点的球面距离.
(1)求证:A、B、C、D、E五点都在以AB为直径的同一球面上.
(2)若∠CBE=90° CE= 
AD=1 求B、D两点的球面距离.
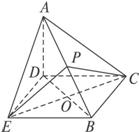
(1)证明:取AB中点P
由题设条件知△AEB、△ADB、△ABC都是直角三角形
故PE=PD=PC= AB=PA=PB 所以A、B、C、D、E五点在同一球面上.
(2)解析:由题意知BCDE是矩形 所以BD=CE= 
.
在Rt△ADB中 AB=2 AD=1
所以∠DPB=120° D、B的球面距离为 
.
如图▱ABCD，以D为圆心，AD为半径的圆交AB，CD于E、F，延长AD交⊙D于G，（1）求证：弧 2020-05-16 …
如图,△ABC≌△A'B'C',AD,A'D'分别是△ABC,△A'B'C'的对应边上的中线.AD 2020-05-16 …
已知,如图,AD、A'D'分别为△ABC和△A'B'C'的角平分线.且AD=A'D',∠B=∠B' 2020-05-23 …
三角形ABC是等边三角形,AM⊥BC于M,PD⊥AD于D,PE⊥AC于E,PD=h1,PE=h2, 2020-06-04 …
全等三角形的数学题1.AB=AC.BD=CE/角B=角C.证明:AD=AE2.AB//CD.点C是 2020-06-27 …
己知,AD平行BC,角1等于角2,角3等于角4,直线CD过点E交AD于D,交BC于点C,求证,AD 2020-07-08 …
问一个关于全等三角形的问题三角形ABC与三角形A'B'C'中两个三角形都是锐角三角形AB=A'B' 2020-07-19 …
已知三角形ABC全等于三角形A'B'C',AD,A'D'分别是三角形ABC和三角形A'B'C'的角 2020-07-22 …
如图AD∥BC，∠1=∠2，∠3=∠4，直线DC过点E交AD于D，交BC于点C．求证：AD+BC= 2020-08-01 …
证明相似三角形的高三角形ABC相似三角形A'B'C'相似比为K,AD,A'D'分别是三角形ABC和 2020-08-01 …