早教吧作业答案频道 -->数学-->
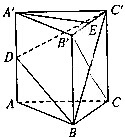
如图，已知直三棱柱ABC-A′B′C′的底面为等边三角形，D是AA′上的点，E是B′C′的中点，且A′E∥平面DBC′，试判断点D在AA′上的位置，并给出证明．
题目详情
如图，已知直三棱柱ABC-A′B′C′的底面为等边三角形，D是AA′上的点，E是B′C′的中点，且A′E∥平面DBC′，试判断点D在AA′上的位置，并给出证明．
▼优质解答
答案和解析
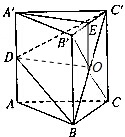D点是AA′的中点．理由如下：
如图，取BC的中点O，连接EO，DO，
∵直三棱柱ABC-A′B′C′的底面为等边三角形，E是B′C′的中点，
∴EO∥BB′∥AA′．
又∵A′E∥平面DBC′，
∴A′E∥DO．
∴四边形A′DOE是平行四边形，
∴A′D=EO，
∴D点是AA′的中点．
D点是AA′的中点．理由如下：如图，取BC的中点O，连接EO，DO，
∵直三棱柱ABC-A′B′C′的底面为等边三角形，E是B′C′的中点，
∴EO∥BB′∥AA′．
又∵A′E∥平面DBC′，
∴A′E∥DO．
∴四边形A′DOE是平行四边形，
∴A′D=EO，
∴D点是AA′的中点．
看了 如图，已知直三棱柱ABC-A...的网友还看了以下：
如果梯形的对角互补,最大角是最小角的3倍,上底为a,下底为b（b＞a）,则两底间的距离为A：a+b 2020-04-26 …
(1)已知log3为底7=a,log3为底4=b,求log12为底21(用a,b表示)(2)已知l 2020-06-11 …
五年级数学简易方程两面三角形的旗子,其中A面旗的底是B面旗对应底的2倍,A面旗底上的高是B面旗对应 2020-06-27 …
如图,我们知道两个完全相同的梯形可以拼成一个平行四边形,设梯形的上底为a,下底为b,高为h,则得到 2020-07-18 …
1.已直Lg2=a,lg3=b,试用a,b表示log512（5是底数,12是真数）2.若a+b=( 2020-07-30 …
实数a、b、c都属于区间(0,1),且a、b、c互不相等,...已知实数a、b、c都属于区间(0,1 2020-11-01 …
已知向量a.b.c.是空间的一个单位正交基底、向量a+b.a-b.c.是空间的另一个基底、若向量p在 2020-11-10 …
（2012•滁州模拟）一个等腰梯形，上底是a分米，下底是b分米，高h分米．沿着底边上的高把它分成两部 2020-11-12 …
请问,已知一个正梯形的上底是a,下底是b,高是h,求这个梯形的周长.还有平行四边形,已知上底是a,下 2020-12-25 …
如图，一架25米的梯子AB靠在一座建筑物AO上，梯子的底部B距离建筑物AO的底部O有7米（即BO=7 2021-01-19 …