早教吧作业答案频道 -->数学-->
如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB=2a,CE=2CD.(1)求证:平面CDE⊥平面ADE;(2)求多面体ABCDE的体积.
题目详情
如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB=2a,CE=
CD.
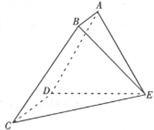
(1)求证:平面CDE⊥平面ADE;
(2)求多面体ABCDE的体积.
| 2 |

(1)求证:平面CDE⊥平面ADE;
(2)求多面体ABCDE的体积.
▼优质解答
答案和解析
证明:(1)∵CD=DE,CE=
CD,
∴CD2+DE2=CE2,
∴CD⊥DE,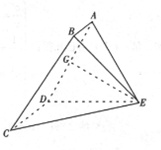
又CD⊥AD,AD⊂平面ADE,DE⊂平面ADE,AD∩DE=D,
∴CD⊥平面ADE,又CD⊂平面CDE,
∴平面CDE⊥平面ADE.
(2)过E作EG⊥AD,垂足为G,
∵CD⊥平面ADE,GE⊂平面ADE,
∴CD⊥GE,
又GE⊥AD,AD⊂平面ABCD,CD⊂平面ABCD,AD∩CD=D,
∴GE⊥平面ABCD.
∵△ADE是等边三角形,DE=2a,
∴GE=
a.
∵S梯形ABCD=
(AB+CD)•AD=
×(a+2a)•2a=3a2.
∴多面体ABCDE的体积V=VE-ABCD=
S梯形ABCD•EG=
×3a2×
a=
a3.
| 2 |
∴CD2+DE2=CE2,
∴CD⊥DE,

又CD⊥AD,AD⊂平面ADE,DE⊂平面ADE,AD∩DE=D,
∴CD⊥平面ADE,又CD⊂平面CDE,
∴平面CDE⊥平面ADE.
(2)过E作EG⊥AD,垂足为G,
∵CD⊥平面ADE,GE⊂平面ADE,
∴CD⊥GE,
又GE⊥AD,AD⊂平面ABCD,CD⊂平面ABCD,AD∩CD=D,
∴GE⊥平面ABCD.
∵△ADE是等边三角形,DE=2a,
∴GE=
| 3 |
∵S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴多面体ABCDE的体积V=VE-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
看了 如图,在空间多面体ABCDE...的网友还看了以下:
(2014•义乌市三模)在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶 2020-05-14 …
O、A、B、C为空间四个点,又OA、OB、OC为空间的一个基底,则()A.O、A、B、C四点不共线 2020-05-14 …
因式分解a3(b-c)+b3(c-a)+c3(a-b)如果用待定系数法解,得a3(b-c)+b3( 2020-05-16 …
关于图中铁路线及铁路枢纽的说法正确的是()A.四图中的铁路枢纽都是省会城市B.由沈阳至南京便捷的铁 2020-06-21 …
1、昏君亡国,明君兴政.参照这一标准,下列四人中,与其他三人明显不同的是1、昏君亡国,明君兴政.参 2020-06-29 …
一道MBA有关等比数列数学题po是以a为边长的正方形,p1是po的四边中点为顶点的正方形,p2是p 2020-07-04 …
如图,长方形OABC中,点A坐标为(-3,0),点B坐标为(-3,2),C点坐标为(0,2).(1 2020-07-22 …
直接写口数c.6÷c.6=6.3×c.四=12.五×c.8=1c÷c.五=c.8÷c.c4=c.42 2020-10-31 …
甲、乙、丙、丁四人中有两人在假日为街道做好事,班主任把四人找来了解情况,四人分别回答如下:甲:丙、丁 2020-11-04 …
读“我国南极地区四个科学考察站示意图”,判断下列叙述正确的是()A.四个科考站都建在南极圈以内B.2 2020-11-06 …