如图1，线段AB=12厘米，动点P从点A出发向点B运动，动点Q从点B出发向点A运动，两点同时出发，到达各自的终点后停止运动．已知动点Q运动的速度是动点P运动的速度的2倍．设两点之间的距离

Question

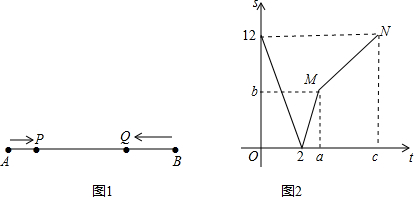
如图1，线段AB=12厘米，动点P从点A出发向点B运动，动点Q从点B出发向点A运动，两点同时出发，到达各自的终点后停止运动．已知动点Q运动的速度是动点P运动的速度的2倍．设两点之间的距离为s（厘米），动点P的运动时间为t（秒），图2表示s与t之间的函数关系．
（1）求动点P、Q运动的速度；
（2）图2中，a=___，b=___，c=___；
（3）当a≤t≤c时，求s与t之间的函数关系式（即线段MN对应的函数关系式）．

Answer 1

（1）设动点P运动的速度为x厘米/秒，则动点Q运动的速度为2x厘米/秒，
根据题意，得2（x+2x）=12，
解得x=2．
答：动点P、Q运动的速度分别是2厘米/秒、4厘米/秒；

（2）动点Q运动的时间a=(12)/(4)=3；
经过3秒，动点Q从点B运动到点A，此时动点P运动的路程为2×3=6，即b=6；
动点P运动的时间c=(12)/(2)=6；
故答案为3，6，6；

（3）当3≤t≤6时，设s与t之间的函数关系式为s=kt+b，
∵图象过点（3，6），（6，12），
∴

3k+b=6

6k+b=12

，
解得

k=2

b=0

，
∴s与t之间的函数关系式为s=2t（3≤t≤6）．