早教吧作业答案频道 -->数学-->
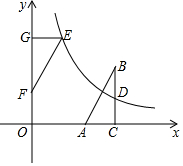
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=kx(k>0)的图象经过BC边的中点D(3,1)(1)求这个反比例函数的表达式;(2)若△ABC与△EFG成中心对称
题目详情
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=
(k>0)的图象经过BC边的中点D(3,1)
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
| k |
| x |

(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
▼优质解答
答案和解析
(1)∵反比例函数y=
(k>0)的图象经过点D(3,1),
∴k=3×1=3,
∴反比例函数表达式为y=
;
(2)①∵D为BC的中点,
∴BC=2,
∵△ABC与△EFG成中心对称,
∴△ABC≌△EFG,
∴GF=BC=2,GE=AC=1,
∵点E在反比例函数的图象上,
∴E(1,3),即OG=3,
∴OF=OG-GF=1;
②如图,连接AF、BE,
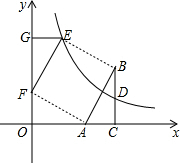
∵AC=1,OC=3,
∴OA=GF=2,
在△AOF和△FGE中
∴△AOF≌△FGE(SAS),
∴∠GFE=∠FAO=∠ABC,
∴∠GFE+∠AFO=∠FAO+∠BAC=90°,
∴EF∥AB,且EF=AB,
∴四边形ABEF为平行四边形,
∴AF=EF,
∴四边形ABEF为菱形,
∵AF⊥EF,
∴四边形ABEF为正方形.
(1)∵反比例函数y=
| k |
| x |
∴k=3×1=3,
∴反比例函数表达式为y=
| 3 |
| x |
(2)①∵D为BC的中点,
∴BC=2,
∵△ABC与△EFG成中心对称,
∴△ABC≌△EFG,
∴GF=BC=2,GE=AC=1,
∵点E在反比例函数的图象上,
∴E(1,3),即OG=3,
∴OF=OG-GF=1;
②如图,连接AF、BE,

∵AC=1,OC=3,
∴OA=GF=2,
在△AOF和△FGE中
|
∴△AOF≌△FGE(SAS),
∴∠GFE=∠FAO=∠ABC,
∴∠GFE+∠AFO=∠FAO+∠BAC=90°,
∴EF∥AB,且EF=AB,
∴四边形ABEF为平行四边形,
∴AF=EF,
∴四边形ABEF为菱形,
∵AF⊥EF,
∴四边形ABEF为正方形.
看了 如图,在直角坐标系中,Rt△...的网友还看了以下:
如图(1),在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6) 2020-03-29 …
刚刚学...(我代我同学问来着..)1.已知直角三角形的两条直角边为a和b.斜边为c.(1)如果a= 2020-03-30 …
在△ABC中,AB=5cm,BC=4cm,AC=3cm(1)若以C为圆心,2cm长为半径画⊙C,则 2020-04-26 …
下面四个命题中,正确的是①如果直线a‖c,b‖c,那么a、b可以确定一个平面.②如果直线a和b都与 2020-04-27 …
如果向量a,b,c共面,b,c,d也共面,那么a,b,c,d是否共面?如果不一定共面,请举例说明浪 2020-05-13 …
如图J1-11,直线a,b被c,d所截,且c垂直于a,c垂直于b,角1=70度,求角2的度数 2020-05-16 …
公安机关必须置于党委( )领导之下。A.形式的、直接的B.实际的、直接的C.形式的、间接的D.实际的 2020-05-19 …
近因是指导致损害发生的()原因A.时间上最近的B.最直接的C.起决定作用的D.起支配作用的E.空间上 2020-05-22 …
如图所示,垂直纸面放置的两根固定长直导线a和b中通有大小相等的稳恒直流电流I,在a、b连线的中垂线 2020-06-14 …
如果三角形ABC中角ACB等于90度DA垂直于ABFE垂直于DECB分别在DEEF上CA垂直于AF 2020-06-15 …