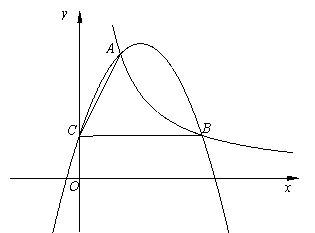
如图，点A（2，6）和点B（点B在点A的右侧）在反比例函数的图像上，点C在轴上，BC//轴，，二次函数的图像经过A、B、C三点．（1）

Question

如图，点 A （ 2 ， 6 ）和点 B （点 B 在点 A 的右侧）在反比例函数的图像上，点 C 在 轴上， BC // 轴， ，二次函数的图像经过 A 、 B 、 C 三点．

（1）   求反比例函数和二次函数的解析式；

（2） 如果点 D 在 轴的正半轴上，点 E 在反比例函数的图像上，四边形 ACDE 是平行四边形，求边 CD 的长．

 

Answer 1

解 ：（ 1 ）设 反比例函数的解析式为 ．

          ∵ 点 A （ 2 ， 6 ）在反比例函数的图像上，∴ 6= ，

∴ ，∴ 反比例函数的解析式为 ．

      作 AM ⊥ BC ，垂足为 M ，交 轴于 N ，∴ CM =2 ．

在 Rt △ ACM 中， ．

∵ BC // 轴 ， OC = AN – AM =6 – 4=2 ，∴ 点 C 的坐标 （ 0 ， 2 ）．

当 时， ，∴ 点 B 的坐标（ 6 ， 2 ）

设 二次函数的解析式为 ，

∴   ∴ 二次函数的解析式为 ．

（ 2 ）延长 AC 交 轴于 G ，作 EH ⊥ 轴，垂足为 H ．

∵在 □ ACDE 中， AC // DE ，∴∠ AGO = ∠ EDH ．

∵ BC // 轴，∴∠ ACM = ∠ AGO ．∴∠ ACM = ∠ EDH ．

∵∠ AMC = ∠ EHD =90 º， AC = ED ，∴△ ACM ≌△ EDH ．

∴ EH = AM =4 ， DH = CM =2 ．∴点 E （ 3 ， 4 ）．

∴ OE =3 ， OD = OE – DH =1

∴ CD= ．