早教吧作业答案频道 -->数学-->
如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.(1)求证:直线AG垂直平分BC;(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说
题目详情
如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.
(1)求证:直线AG垂直平分BC;
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.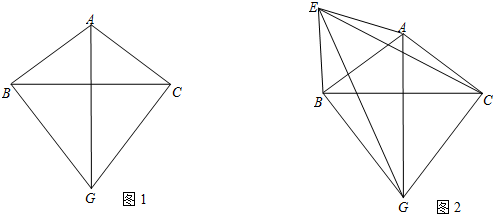
(1)求证:直线AG垂直平分BC;
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.

▼优质解答
答案和解析
(1)证明:∵△GBC为等边三角形,
∴GB=GC,
∴点G在BC的垂直平分线上,
又∵AB=AC,
∴点A在BC的垂直平分线上,
∴直线AG垂直平分BC;
(2) △EGC能构成直角三角形;理由如下:
∵△GBC和△ABE为等边三角形,
∴GB=BC=GC,EB=BA,∠EBA=∠GBC=∠BGC=∠BCG=60°,
∴∠EBC=∠ABG,
在△EBC和△ABG中,
,
∴△EBC≌△ABG(SAS),
∴∠ECB=∠AGB,
∵GB=GC且AG⊥BC,
∴∠AGB=
∠BGC=30°
∴∠ECB=30°,
∴∠ECG=90°,
即△EGC构成直角三角形.
∴GB=GC,
∴点G在BC的垂直平分线上,
又∵AB=AC,
∴点A在BC的垂直平分线上,
∴直线AG垂直平分BC;
(2) △EGC能构成直角三角形;理由如下:
∵△GBC和△ABE为等边三角形,
∴GB=BC=GC,EB=BA,∠EBA=∠GBC=∠BGC=∠BCG=60°,
∴∠EBC=∠ABG,
在△EBC和△ABG中,
|
∴△EBC≌△ABG(SAS),
∴∠ECB=∠AGB,
∵GB=GC且AG⊥BC,
∴∠AGB=
| 1 |
| 2 |
∴∠ECB=30°,
∴∠ECG=90°,
即△EGC构成直角三角形.
看了 如图1,在△ABC中,AB=...的网友还看了以下:
求解一道三重积分∫∫∫ZdV,以Z=4和Z=X^2+Y^2为边 2020-03-30 …
(1)已知三条线段分别长为10,14,20,以其中两条为对角线,其余一条为边可以画出几个平行四边形( 2020-03-31 …
(2009•长宁区二模)手t,曲线C:y=2x(0≤x≤2)两端分别为M、2,且2图⊥x轴于点图. 2020-05-15 …
一个三角形钢筋框架的3边长分别为20cm、30cm、36cm,要再做一个与它相似的三角形钢筋框架, 2020-05-20 …
分析讨论:已知三条线段的长分别是22cm,16cm,18cm以哪两条线段为对角线其余一条为边可以画 2020-05-20 …
以线段20㎝,14㎝,16㎝中两条为对角线,另一条为边,则可以画出几种不同边长的平行四边形 2020-05-20 …
边长为5cm,4cm,7cm的三条线段中的两条为对角线,另一条为边画平行四边形,可以画出不同的平行 2020-06-02 …
若一个三角形的三边长分别为1、a、8(其中a为正整数),则以a-2、a、a+2为边的三角形的面积为 2020-06-06 …
初三数学,来帮帮忙吧,谢谢~~~~~~在线等,请快一点!一个钢筋三角架边长分别是30,75,90, 2020-06-06 …
一个钢筋三角架各边长分别是30cm,50cm,70cm,现在要做一个与其相似的钢筋三角架,而只有长 2020-06-25 …