早教吧作业答案频道 -->数学-->
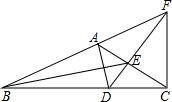
如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.
题目详情
如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.

▼优质解答
答案和解析
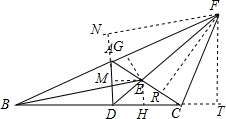 过F作FN⊥AD于N,FR⊥AC于R,FT⊥BC于T,过E作EM⊥AD于M,EH⊥BC于H,EG⊥AB于G,
过F作FN⊥AD于N,FR⊥AC于R,FT⊥BC于T,过E作EM⊥AD于M,EH⊥BC于H,EG⊥AB于G,
∵∠BAC=120°,AD为△ABC的内角平分线,
∴∠FAN=∠BAD=60°,∠RAF=60°,
在△AFN与△AFR中,
,
∴△AFN≌△AFR,
∴FN=FR,
∵CF为△ABC的外角平分线,
∴FR=FT,
∴NF=FT,
∴DF平分∠ADC,
∴ME=EH,
∵∠DAC=∠CAF=60°,
∴EG=EM,
∴EG=EH,
∴BE平分∠ABC.
 过F作FN⊥AD于N,FR⊥AC于R,FT⊥BC于T,过E作EM⊥AD于M,EH⊥BC于H,EG⊥AB于G,
过F作FN⊥AD于N,FR⊥AC于R,FT⊥BC于T,过E作EM⊥AD于M,EH⊥BC于H,EG⊥AB于G,∵∠BAC=120°,AD为△ABC的内角平分线,
∴∠FAN=∠BAD=60°,∠RAF=60°,
在△AFN与△AFR中,
|
∴△AFN≌△AFR,
∴FN=FR,
∵CF为△ABC的外角平分线,
∴FR=FT,
∴NF=FT,
∴DF平分∠ADC,
∴ME=EH,
∵∠DAC=∠CAF=60°,
∴EG=EM,
∴EG=EH,
∴BE平分∠ABC.
看了 如图,△ABC中,∠BAC=...的网友还看了以下:
当a、b满足什么条件时,下列关系成立:(1)|a+b|=|a|+|b|;(2)|a+b|=||a| 2020-06-12 …
积分第一中值定理的推广f(x)g(x)在a,b连续.g(x)不变号,求证:存在一点e∈a,b使∫( 2020-06-14 …
公式a*b/(a-1)还能解吗公式a*b*(a-1)=a*b*a-a*b这个成立,公式a*b/(a 2020-07-17 …
在你2011-08-13有一题的解答我有点不懂设a,b属于R,集合A中有3元素,1,a+b,a,集 2020-07-20 …
已知向量a与b反向,下列等式成立的是:A:|a|-|b|=|a-b|B:|a+b|=|a-b已知向 2020-07-30 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
数学绝对值不等式|a|-|b|≤|a±b|≤|a|+|b|中的±要怎么理解|a|-|b|≤|a±b 2020-08-03 …
阅读:例:已知1/a+1/b=5/a+b,求b/a+a/b的值.因为1/a+1/b=5/a+b,所以 2020-11-15 …
已知:n=1a^2-b^2=(a-b)(a+b);a^3-b^3=(a-b)(a^2+ab+b^2) 2020-12-23 …
设A,B为任意两个事件且A⊂B,P(B)>0,则下列选项必然成立的是()A.P(A)<P(A|B)B 2021-01-01 …