早教吧作业答案频道 -->数学-->
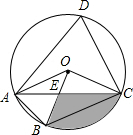
如图,四边形ABCD是O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=23,则图中阴影部分面积是(结果保留π和根号)
题目详情
如图,四边形ABCD是 O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2
,则图中阴影部分面积是___(结果保留π和根号)
| | 3 |

▼优质解答
答案和解析
∵四边形ABCD是 O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2
,
∴OE=OC•tan∠OCE=2
•tan30°=2
×
=2,
∴S△OEC=
OE•OC=
×2×2
=2
,
∴S扇形OBC=
=3π,
∴S阴影=S扇形OBC-S△OEC=3π-2
.
故答案为:3π-2
.
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2
| 3 |
∴OE=OC•tan∠OCE=2
| 3 |
| 3 |
| ||
| 3 |
∴S△OEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S扇形OBC=
90•π×(2
| ||
| 360 |
∴S阴影=S扇形OBC-S△OEC=3π-2
| 3 |
故答案为:3π-2
| 3 |
看了 如图,四边形ABCD是O的内...的网友还看了以下:
AB为圆O直径,AD与圆O相切于A·(初3圆的几何)AB为圆O直径,AD与圆O相切于A,DE与圆O 2020-05-20 …
一道难题,谁能帮我解在某海滨城市,曲线MN为海岸线,直线l为一条南北方向的公路.O为某城市中心,小 2020-06-10 …
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,点B在⊙O上,BP的延 2020-07-13 …
如图已知直线l与圆o相离,OA垂直l于点A,OA与圆O相交于点B用户名:小智怡|分类:1分钟前如图 2020-07-26 …
已知圆O:x2+y2=r2,点P(a,b)(ab≠0)是圆O内一点,过点P的圆O的最短弦所在的直线 2020-07-26 …
如图,已知直线l与O相离,OA⊥l于点A,OA=5,OA与O相交于点P,AB与O相切于点B,BP的 2020-07-26 …
已知圆O:x2+y2=r2,点P(a,b)(ab≠0)是圆O内一点,过点P的圆O的最短弦所在的直线 2020-07-31 …
相似三角形问题已知圆O与圆A相交于C,D两点.A,O分别是两圆的圆心,三角形ABC内界于圆O,弦C 2020-08-03 …
如图1,BC是O的直径,点A在O上,点D在CA的延长线上,DE⊥BC,垂足为点E,DE与O相交于点H 2020-11-03 …
求2009年的济南的中考数学题:已知AB是圆O的直径,CA与圆O相切于点A,连接CO交圆O于点D,C 2021-01-22 …