早教吧作业答案频道 -->数学-->
如图,已知四边形ABCD是O的内接四边形,过点A的切线与CB的延长线交于点P,且PA=82,PB=8.(1)若∠APB=45°求∠D的大小;(2)若O的半径为5,求圆心O到直线BC的距离.
题目详情
如图,已知四边形ABCD是 O的内接四边形,过点A的切线与CB的延长线交于点P,且PA=8
,PB=8.
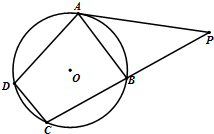
(1)若∠APB=45°求∠D的大小;
(2)若 O的半径为5,求圆心O到直线BC的距离.
| 2 |

(1)若∠APB=45°求∠D的大小;
(2)若 O的半径为5,求圆心O到直线BC的距离.
▼优质解答
答案和解析
(1)在△PAB中,有PA=8
,PB=8,∠APB=45°.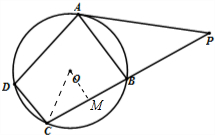
由余弦定理得:AB2=82+(8
)2-2×8×8
cos45°=64,解得AB=8.
∴AB=PB,∠BAP=45°,
∴∠ABP=Rt∠.
所以△PAB为Rt△,即AB⊥PC.
所以∠ABC=90°,
又因为四边形ABCD是 O的内接四边形,
所以∠D=90°.
(2)连接OC,作OM⊥BC于M,
由垂径定理可知:M为BC的中点,
由切割线定理得:PA2=PB•PC,
又PA=8
,PB=8,
所以PC=16,BC=8,MC=4.
因为 O的半径为5,所以在Rt△OMT中有,OM=3,
所求圆心O到直线BC的距离为3.
| 2 |

由余弦定理得:AB2=82+(8
| 2 |
| 2 |
∴AB=PB,∠BAP=45°,
∴∠ABP=Rt∠.
所以△PAB为Rt△,即AB⊥PC.
所以∠ABC=90°,
又因为四边形ABCD是 O的内接四边形,
所以∠D=90°.
(2)连接OC,作OM⊥BC于M,
由垂径定理可知:M为BC的中点,
由切割线定理得:PA2=PB•PC,
又PA=8
| 2 |
所以PC=16,BC=8,MC=4.
因为 O的半径为5,所以在Rt△OMT中有,OM=3,
所求圆心O到直线BC的距离为3.
看了 如图,已知四边形ABCD是O...的网友还看了以下:
ob.oc是圆o的半径,a是圆o上一点,若已知角b=20,角c=30,求角a的度数 2020-03-30 …
圆的面积与它的半径,圆的周长与它的半径A.成正比例B.成反比例C.不成比例. 2020-04-11 …
如图,AC是圆O的直径,PA切圆O于点A,点B是圆O上的一点,且角BAC等于三十度,角APB等于六 2020-04-12 …
如图,PA,PB切O于A,B两点,CD切O于点E,交PA,PB于C,D.延长BO交PA的延长线于点 2020-04-12 …
1、半径等于12的圆中,垂直平分半径的弦长为()A、3√6B、12√3C、6√3D、18√32、P 2020-04-12 …
1.PT切圆O于T,CT为直径,D为OC上的一点,支线PD交圆O于B和A,B在线段PD上,若CD= 2020-04-12 …
如图,PA,PB是圆0的切线,切点分别为A,B,已知,角APB等于60度,PA等于3.1.求圆0的 2020-04-27 …
已知圆o的半径为1,pa,pb为它的两条切线,a,b为切点.求向量pa与向量pb的内积的最小值. 2020-05-14 …
初三数学题(拓展部分)直线与圆的关系已知PA、PB是圆O的两条切线,切点分别为A、B,点C、D分别 2020-05-21 …
已知圆A的半径为3cm,圆B的半径为5CM,AB=14cm,p是线段AB上的一点,以p为圆心作圆p 2020-05-22 …