早教吧作业答案频道 -->数学-->
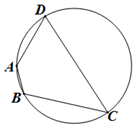
如图,在圆内接四边形ABCD中,AB=1,AD=2.(I)若BD=7,求角C;(II)若BC=3,CD=4,求四边形ABCD的面积.
题目详情
如图,在圆内接四边形ABCD中,AB=1,AD=2.
(I)若BD=
,求角C;
(II)若BC=3,CD=4,求四边形ABCD的面积.
(I)若BD=
| 7 |
(II)若BC=3,CD=4,求四边形ABCD的面积.

▼优质解答
答案和解析
(本题满分为12分)
(I)在△ABD中,由余弦定理得,cosA=
=-
.
又0<A<π,
∴A=
.
∵四边形ABCD是圆的内接四边形,
∴C=π-A=
.…(6分)
(II)因为BD2=AB2+AD2-2AB•AD•cosA=5-4cosA,
且BD2=CB2+CD2-2CB•CD•cos(π-A)=25+24cosA,
∴cosA=-
.…(9分)
又0<A<π,
∴sinA=
=
.
∴S△BCD=S△ABD+S△CBD=
AB•AD•sinA+
CB•CD•sin(π-A)=2
.…(12分)
(I)在△ABD中,由余弦定理得,cosA=
| AD2+AB2-BD2 |
| 2AD•AB |
| 1 |
| 2 |
又0<A<π,

∴A=
| 2π |
| 3 |
∵四边形ABCD是圆的内接四边形,
∴C=π-A=
| π |
| 3 |
(II)因为BD2=AB2+AD2-2AB•AD•cosA=5-4cosA,
且BD2=CB2+CD2-2CB•CD•cos(π-A)=25+24cosA,
∴cosA=-
| 5 |
| 7 |
又0<A<π,
∴sinA=
| 1-cos2A |
2
| ||
| 7 |
∴S△BCD=S△ABD+S△CBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
看了 如图,在圆内接四边形ABCD...的网友还看了以下:
下列条件中不能确定四边形ABCD是平行四边形的是()A.AB=CD,AD∥BCB.AB=CD,AB∥ 2020-03-31 …
1.若A,B,C,D是不共线的四点,则向量AB=向量CD是四边形ABCD为平行四边形的充要条件是正 2020-04-26 …
圆O的直径AB=12cm,有条定长为8cm的动弦CD在弧AB上滑动(C与A不重合),CE垂直CD交 2020-05-16 …
不能判定四边形ABCD是平行四边形的是()下列条件不能判定四边形ABCD是平行四边形的是()A.A 2020-05-23 …
在圆O中,AB是直径,CD是弦,AB垂直于CD,若P'在劣弧CD上(不与C、D重合)时,角CP'D 2020-07-14 …
利用matlab计算四杆机构通过方程matlab计算,假设AD=BC=600mm,AB=200mm 2020-07-24 …
扇形AOB中圆心角AOB=90度半径为2,E为弧AB中点,C,D为弧AB上的动点,且CD平行AB, 2020-08-01 …
已知AB为圆的直径,CD垂直AB与圆交于C,垂足为D,以C为圆心,CD为半径作圆与前圆交于EF,EF 2020-11-27 …
四边形ABCD中,对角线AC,BD相交于点O,给出下列四组条件:①AB//CD,AD//BC②AB= 2020-12-23 …
如图,四边形EFGH为空间四边形ABCD的一个截面,四边形EFGH为平行四边形.(1)求证:AB∥平 2020-12-25 …