早教吧作业答案频道 -->数学-->
(本题证明值可直接利用如下结论:若公共边所对的两个张角相等,则相应的四点共圆.例如如图1,由∠ACB=∠ADB,可得四点A、B、C、D共圆)如图2,圆内接五边形ABCDE中,AD是外接圆的
题目详情
(本题证明值可直接利用如下结论:若公共边所对的两个张角相等,则相应的四点共圆.例如如图1,由∠ACB=∠ADB,可得四点A、B、C、D共圆)如图2,圆内接五边形ABCDE中,AD是外接圆的直径,BE⊥AD,垂足为H,过点H作平行于CE的直线,与直线AC,DC分别交于F,G.证明:
(1)点A,B,F,H共圆;
(2)四边形BFCG是矩形.
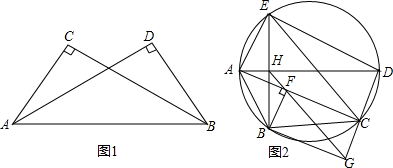
(1)点A,B,F,H共圆;
(2)四边形BFCG是矩形.

▼优质解答
答案和解析
考点:
四点共圆
专题:
分析:
(1)根据圆周角定理得出,∠BAF=∠BEC,结合平行线的性质得出∠BAF=∠BHF,即可得出答案;(2)根据四点共圆的性质得出∠BFG=∠DAB=∠BCG,进而得出B、G、F、H共圆,即可得出BG⊥GC,进而得出答案.
证明:(1)由HG∥CE,得∠BHF=∠BEC,又∵BC=BC,∴∠BAF=∠BEC,∴∠BAF=∠BHF,∴点A、B、F、H共圆;(2)由(1)的结论,得∠BHA=∠BFA,∵BE⊥AD,∴BF⊥AC,又∵AD是圆的直径,∴CG⊥AC,由A、B、C、D共圆及A、B、F、H共圆,∴∠BFG=∠DAB=∠BCG,∴B、G、F、H共圆,∴∠BGC=∠AFB=90°,∴BG⊥GC,∴四边形BFCG是矩形.
点评:
此题主要考查了四点共圆的性质以及四点共圆的证明,正确应用四点共圆的性质是解题关键.
考点:
四点共圆
专题:
分析:
(1)根据圆周角定理得出,∠BAF=∠BEC,结合平行线的性质得出∠BAF=∠BHF,即可得出答案;(2)根据四点共圆的性质得出∠BFG=∠DAB=∠BCG,进而得出B、G、F、H共圆,即可得出BG⊥GC,进而得出答案.
证明:(1)由HG∥CE,得∠BHF=∠BEC,又∵BC=BC,∴∠BAF=∠BEC,∴∠BAF=∠BHF,∴点A、B、F、H共圆;(2)由(1)的结论,得∠BHA=∠BFA,∵BE⊥AD,∴BF⊥AC,又∵AD是圆的直径,∴CG⊥AC,由A、B、C、D共圆及A、B、F、H共圆,∴∠BFG=∠DAB=∠BCG,∴B、G、F、H共圆,∴∠BGC=∠AFB=90°,∴BG⊥GC,∴四边形BFCG是矩形.
点评:
此题主要考查了四点共圆的性质以及四点共圆的证明,正确应用四点共圆的性质是解题关键.
看了 (本题证明值可直接利用如下结...的网友还看了以下:
在底面直径和高均为3的圆锥内作一内接圆柱,当内接圆柱体积最大时该圆柱的侧面积为()A.πB.2πC 2020-05-14 …
△ABC的三条边长分别是3,4,5,点P为△ABC内接圆上一点,求PA+PB+PC的最大值,最小值 2020-05-23 …
一些图形或者体的外接圆,内接圆,外接球,内接球的公式比如,边长为a正四面体的内接球,外接球半径各是 2020-07-15 …
任意三角形的内接圆半径公式,和外接圆半径公式是什么啊?不要什么RT三角形的.给你abc三边,用公式 2020-07-26 …
在底面半径为R,高为h的圆锥内有一内接圆柱,则内接圆柱的圆柱的高为时,其侧面积最大值为. 2020-07-26 …
如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).(1 2020-07-26 …
△ABC中,∠C=90°,两条直角边分别为5,12,求它的外接圆的半径,外接圆与内接圆两圆心的距离 2020-08-01 …
已知圆的半经长为2cm用圆规和直尺作这个圆的内接正六边形并求正六边形的内接圆半径外接圆半径及中心角 2020-08-01 …
初三关于圆的数学题一个等边三角形,边长为a它有一个内接圆和一个外接圆,求内接圆与外接圆不重叠的部分 2020-08-03 …
已知圆锥高为H,底面半径为R,则它的内接圆柱的高为x,则这个内接圆柱的侧面积为,当x=时,内接圆柱的 2021-02-17 …