早教吧作业答案频道 -->数学-->
在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE(如图①),连接AD,BE,易证明BE=AD.(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由
题目详情
在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE(如图①),连接AD,BE,易证明BE=AD.
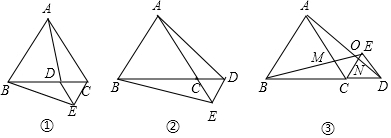
(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由;
(2)在图②中,若等边三角形CDE与等边三角形ABC均在直线BC的同一侧(如图③),并且B,C,D三点在同一直线上,猜想BE=AD是否依然成立?试说明理由;
(3)在(2)的条件下,根据图汇总所标字母,请直接写出你发现的两个正确结论.
①___;②___.

(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由;
(2)在图②中,若等边三角形CDE与等边三角形ABC均在直线BC的同一侧(如图③),并且B,C,D三点在同一直线上,猜想BE=AD是否依然成立?试说明理由;
(3)在(2)的条件下,根据图汇总所标字母,请直接写出你发现的两个正确结论.
①___;②___.
▼优质解答
答案和解析
(1)BE=AD依然成立,
证明:∵△ABC是等边三角形,
∴CA=CB,
∵△CDE是等边三角形,
∴CD=CE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE,
∴BE=AD;
(2)BE=AD成立,
∵△ABC是等边三角形,△CDE是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD,
∴BE=AD;
(3)∵△BCE≌△ACD,
∴∠DAC=∠EBC,
∠AOB=∠EBC+∠ADC=∠EBC+∠BEC=60°,
故答案为:①∠DAC=∠EBC;②∠AOB=60°.
证明:∵△ABC是等边三角形,
∴CA=CB,
∵△CDE是等边三角形,
∴CD=CE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE,
∴BE=AD;
(2)BE=AD成立,
∵△ABC是等边三角形,△CDE是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
|
∴△BCE≌△ACD,
∴BE=AD;
(3)∵△BCE≌△ACD,
∴∠DAC=∠EBC,
∠AOB=∠EBC+∠ADC=∠EBC+∠BEC=60°,
故答案为:①∠DAC=∠EBC;②∠AOB=60°.
看了 在等边三角形ABC的边BC上...的网友还看了以下:
一个平底玻璃筒长25cm底面积为20平方厘米若将其底部插入水下0.1米深处一个平底玻璃筒长25cm底 2020-03-31 …
“天下古今成败之林,若是其莽然不一途也。”此句中的“不一”,应解释为[]A.种种不同B.不等C.不 2020-04-06 …
若a=5+2根号6,b=2根号6-5,则a,b的关系为 A.互为相反数 B.倒数 C.负倒数 D若 2020-05-16 …
下列命题正确的是()A.若函数f(x)在x=a处连续,则函数f(x)在x=a的邻域内连续B.若函数 2020-06-12 …
有三个共力点,大小都是10N,互相间互成120°的夹角,他们的合力为()n若将其有三个共力点,大小 2020-07-03 …
Inta=3,b=5,c=7;If(a>b)a=b;c=a;If(c!=a)c=b;Printf( 2020-07-09 …
若半径为r的圆C,x^2+y^2+Dx+Ey+F=0,的圆心C到直线l:Dx+Ey+F=0的距离为 2020-07-26 …
如图,在四棱锥D′-ABCE中,底面为直角梯形,AB=2BC=2CE=2,且AB⊥BC,AB∥CE 2020-07-31 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
如图是某反应的微观示意图,关于该反应的说法中,不正确的是()A.反应前后,原子种类、数目均不变B.若 2021-01-21 …