早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,将直线y=kx(k≠0)沿y轴向上平移2个单位得到直线l,已知直线l经过点A(-4,0)(1)求直线l的解析式;(2)设直线l与y轴交于点B,在x轴正半轴上任取一点C
题目详情
如图,在平面直角坐标系xOy中,将直线y=kx(k≠0)沿y轴向上平移2个单位得到直线l,已知直线l经过点A(-4,0)
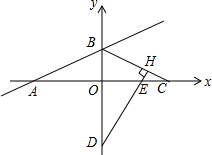
(1)求直线l的解析式;
(2)设直线l与y轴交于点B,在x轴正半轴上任取一点C(OC>2),在y轴负半轴上取点D,使得OD=OC,过D作直线DH⊥BC于H,交x轴于点E,求点E的坐标;
(3)若点P的坐标为(-3,m),△ABP与△ABO的面积之间满足S△ABP=
S△ABO,求m的值.

(1)求直线l的解析式;
(2)设直线l与y轴交于点B,在x轴正半轴上任取一点C(OC>2),在y轴负半轴上取点D,使得OD=OC,过D作直线DH⊥BC于H,交x轴于点E,求点E的坐标;
(3)若点P的坐标为(-3,m),△ABP与△ABO的面积之间满足S△ABP=
| 1 |
| 2 |
▼优质解答
答案和解析
(1)∵将直线y=kx(k≠0)沿y轴向上平移2个单位得到直线l,
∴设直线l解析式为y=kx+2,
∵直线l经过点A(-4,0)
∴-4k+2=0,
∴k=
,
∴直线l的解析式为y=
x+2,
(2)设点C(n,0),(n>2)
∴OC=n.
∵OD=OC,
∴OD=n,
∵点D在y轴负半轴上,
∴D(0,-n),
∵C(n,0),B(0,2),
∴直线BC解析式为y=-
x+2,
∵DH⊥BC,D(0,-n),
∴直线DH的解析式为y=
x-n,
∵点E在x轴上,
∴0=
x-n,
∴x=2,
∴E(2,0);
(3)如图,
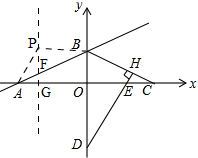
∵A(-4,0),B(0,2),
∴OA=4,OB=2,
∴S△AOB=
OA×OB=
×4×2=4,
S△ABP=
S△ABO=
×4=2,
过点P作y轴的平行线,交AB于F,交x轴于G,
由(1)知,直线AB解析式为y=
x+2,
∵P(-3,m),
∴F(-3,
),
∴PF=|m-
|,
∴S△ABP=S△APF+S△BPF
=
PF×AG+
PF×OG
=
PF×(AG+OG)
=
PF×OA
=
|m-
|×4
=2|m-
|
=2,
∴m=
或m=-
.
∴设直线l解析式为y=kx+2,
∵直线l经过点A(-4,0)
∴-4k+2=0,
∴k=
| 1 |
| 2 |
∴直线l的解析式为y=
| 1 |
| 2 |
(2)设点C(n,0),(n>2)
∴OC=n.
∵OD=OC,
∴OD=n,
∵点D在y轴负半轴上,
∴D(0,-n),
∵C(n,0),B(0,2),
∴直线BC解析式为y=-
| 2 |
| n |
∵DH⊥BC,D(0,-n),
∴直线DH的解析式为y=
| n |
| 2 |
∵点E在x轴上,
∴0=
| n |
| 2 |
∴x=2,
∴E(2,0);
(3)如图,

∵A(-4,0),B(0,2),
∴OA=4,OB=2,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
过点P作y轴的平行线,交AB于F,交x轴于G,
由(1)知,直线AB解析式为y=
| 1 |
| 2 |
∵P(-3,m),
∴F(-3,
| 1 |
| 2 |
∴PF=|m-
| 1 |
| 2 |
∴S△ABP=S△APF+S△BPF
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=2|m-
| 1 |
| 2 |
=2,
∴m=
| 3 |
| 2 |
| 1 |
| 2 |
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
牛三的运用质量为1kg的质点静止在光滑水平面x轴上的原点,先施以x轴正方向的力1N,经历0.1s改 2020-05-21 …
一列在竖直方向振动的简谐横波,波长为λ,沿正x方向传播,某一时刻,在振动位移向上且大小等于振幅一半 2020-06-14 …
在同个平面坐标系中,已知3点坐标,求3点所形成角的方向大概是这样的情况:在一个平面内,左上角为原点 2020-06-14 …
斜抛运动y与x的关系设夹角为α,横坐标为x,纵坐标为y,初速度为v0,那么vx=v0cosα,vy 2020-06-14 …
x,y坐标符号问题当y轴正向向上,x轴正向向右时,处于x轴负半截和y轴正半截区的点的x,y坐标前面 2020-06-14 …
(2014•天津)平衡位置处于坐标原点的波源S在y轴上振动,产生频率为50Hz的简谐横波向x轴正、 2020-06-22 …
如图7,在平面直角坐标系中,已知A(0,2),C(1,0),AB⊥AC,求点B的坐标图是一个坐标A在 2020-11-03 …
一列沿x轴正方向传播的简谱横波在t=0时刻的波形如图所示,质点P的x坐标为3m.已知任意振动质点连续 2020-12-15 …
平衡位置处于坐标原点的波源S在y轴上振动,产生频率为50Hz的简谐横波向x轴正、负两个方向传播,波速 2020-12-15 …
10.一列在竖直方向振动的简谐横波,波长为λ,沿正x方向传播.某一时刻,在振动位移向上且大小等于振幅 2020-12-15 …