早教吧作业答案频道 -->数学-->
如图,已知正方形ABCD和正方形AEFG,连结BE、DG.(1)求证:BE=DG,BE⊥DG;(2)连接BD、EG、DE,点M、N、P分别是BD、EG、DE的中点,连接MP,PN,MN,求证:△MPN是等腰直角三角形;(3)若AB=4
题目详情
如图,已知正方形ABCD和正方形AEFG,连结BE、DG.
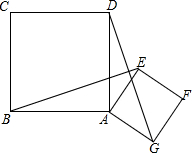
(1)求证:BE=DG,BE⊥DG;
(2)连接BD、EG、DE,点M、N、P分别是BD、EG、DE的中点,连接MP,PN,MN,求证:△MPN是等腰直角三角形;
(3)若AB=4,EF=2
,∠DAE=45°,直接写出MN=___.

(1)求证:BE=DG,BE⊥DG;
(2)连接BD、EG、DE,点M、N、P分别是BD、EG、DE的中点,连接MP,PN,MN,求证:△MPN是等腰直角三角形;
(3)若AB=4,EF=2
| | 2 |
▼优质解答
答案和解析
(1)证明:∵正方形ABCD和正方形AEFG,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAD+∠DAE=∠EAG+∠DAE,
∴∠BAE=∠DAG,
∵在△BEA与△DAG中,
,
∴△BEA≌△DAG(SAS),
∴BE=DG,∠ADG=∠ABE,
∴∠BOD=∠BAD=90°,
∴BE⊥DG;
(2)证明:如图,
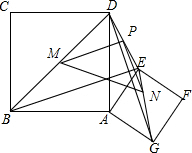
由三角形中位线定理可得:MP∥BE,MP=
BE,
PN∥DG,PN=
DG,
∴PM=PN,∠MPN=∠BOD=90°,
即△MPN是等腰直角三角形;
(3) 如图,
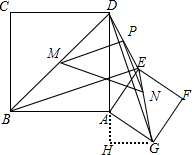
过点G作GH垂直于DA的延长线于点H,
∵∠DAE=45°,∠EAG=90°,
∴∠HAG=45°,
∵EF=2
,
∴AH=HG=2,
∵AB=4,
∴DH=6,
∴DG=
=2
,
∴NP=MP=
,
∴MN=2
.
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAD+∠DAE=∠EAG+∠DAE,
∴∠BAE=∠DAG,
∵在△BEA与△DAG中,
|
∴△BEA≌△DAG(SAS),
∴BE=DG,∠ADG=∠ABE,
∴∠BOD=∠BAD=90°,
∴BE⊥DG;
(2)证明:如图,

由三角形中位线定理可得:MP∥BE,MP=
| 1 |
| 2 |
PN∥DG,PN=
| 1 |
| 2 |
∴PM=PN,∠MPN=∠BOD=90°,
即△MPN是等腰直角三角形;
(3) 如图,

过点G作GH垂直于DA的延长线于点H,
∵∠DAE=45°,∠EAG=90°,
∴∠HAG=45°,
∵EF=2
| 2 |
∴AH=HG=2,
∵AB=4,
∴DH=6,
∴DG=
| 62+22 |
| 10 |
∴NP=MP=
| 10 |
∴MN=2
| 5 |
看了 如图,已知正方形ABCD和正...的网友还看了以下:
已知A(3,-4) B(6,-3) C(5-m,-3-m) ①若A B已知A(3,-4) B(6, 2020-05-16 …
等腰三角形ABC的顶角角A=108度,BC=m,AB=AC=n,记x=(m+n)/(m-n),y= 2020-06-12 …
已知函数f(x)=x^2-(m+1)x+m(m∈R)(1)若tanA,tanB是方程f(x)+4= 2020-06-22 …
已知a=(1,2),b=(m,-1)\x0c(1)若a与b的夹角为3/4派,求m的值?\x0c(2 2020-06-27 …
如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D( 2020-07-22 …
在平面直角坐标系中,△ABC顶点坐标分别为A(0,0),B(1,3√),C(m,0)。若△ABC是 2020-07-30 …
如图,在△ABC外分别以AB,AC为边作正方形ABDE和正方形ACFG,连接EG,AM是△ABC中 2020-08-01 …
数学题目若θ是第二象限角且sinθ=(m-3)/4,求m的取值范围写错了!若θ是第三象限角且sin 2020-08-03 …
(2012•商丘二模)已知两个非零向量a=(m-1,n-1),b=(m-3,n-3),且a与b的夹角 2020-11-12 …
用“三角形”定义新运算,对于任意实数a,b,有a*三角.用“三角形”定义新运算,对于任意实数a,b, 2021-01-20 …