早教吧作业答案频道 -->数学-->
如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.(1)求证:△ABF≌△CBE;(2)判断△CEF的形状,并说明理由.
题目详情
如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
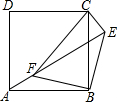
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有
,
∴△ABF≌△CBE(SAS).
(2) △CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°-∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB-∠FEB=135°-45°=90°,
∴△CEF是直角三角形.
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有
|
∴△ABF≌△CBE(SAS).
(2) △CEF是直角三角形.理由如下:

∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°-∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB-∠FEB=135°-45°=90°,
∴△CEF是直角三角形.
看了 如图,点E正方形ABCD外一...的网友还看了以下:
四边形ABCD内接于圆O中,角A=85`,角D=100`,点E在AB的延长线上,求角C,角CBE的 2020-05-13 …
如图,已知角A+角C+角E=180度,求证AB平行EF 2020-05-14 …
正方体ABCD-A'B'C'D',E、F分别是AD、AA的中点 求:直线AB'和EF所成的角的大小 2020-05-16 …
如图,在正方体ABCD-A1B1C1D1中,E为D'C'中点,则二面角E-AB-C的大小为?最好有 2020-05-16 …
正五边形广场ABCDE周长2000m,甲乙两人分别从A,C两点同时出发,沿A—B—C—D—E方向绕 2020-05-16 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
如图7.5-20,求角A+角B+角C+角E+角F的度数? 2020-06-07 …
一个六边形,已知AB平行DE,BC平行EF,CD平行AF,求角A+角C+角E的度数.两种方法 2020-07-21 …
一个六边形,已知AB平行DE、BC平行EF、CD平行AF,求角A+角C+角E的度数.(要有过程)至 2020-07-21 …
BE,CD相交于A点,角C角E的角平分线相交于E点,探究角F角B角D的关系是交于点F````可是米 2020-08-02 …