早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点A的坐标为(4,4).(1)如图1,若点B在x轴正半轴上,点C(1,-1),且AB=BC,AB⊥BC,求点B坐标.(2)如图2,若点B在x轴负半轴上,AE⊥x轴于E,AF⊥y轴于F,∠BFM=4
题目详情
在平面直角坐标系中,点A的坐标为(4,4).
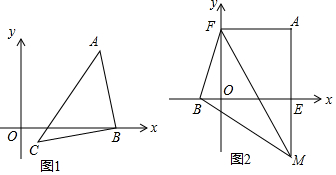
(1)如图1,若点B 在x轴正半轴上,点C(1,-1),且AB=BC,AB⊥BC,求点B坐标.
(2)如图2,若点B在x轴负半轴上,AE⊥x轴于E,AF⊥y轴于F,∠BFM=45°,MF交直线AE于M.求证:OB+BM=AM.
(1)如图1,若点B 在x轴正半轴上,点C(1,-1),且AB=BC,AB⊥BC,求点B坐标.
(2)如图2,若点B在x轴负半轴上,AE⊥x轴于E,AF⊥y轴于F,∠BFM=45°,MF交直线AE于M.求证:OB+BM=AM.

▼优质解答
答案和解析
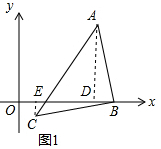 (1) 如图1,过A作AD⊥x轴,CE⊥x轴,垂足分别为D、E.
(1) 如图1,过A作AD⊥x轴,CE⊥x轴,垂足分别为D、E.
∵AD⊥x轴,CE⊥x轴,
∴∠ADB=∠BEC=90°,
∴∠DAB+∠ABD=90°,
∵AB⊥BC,
∴∠EBC+∠ABD=90°,
∴∠DAB=∠EBC,
在△ADB与△BEC中,
,
∴△ADB≌△BEC(AAS),
∴BD=CE,
∵A(4,4),C(1,-1),
∴OD=4,CE=1,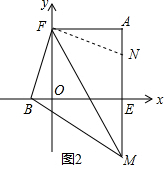
∴OB=OD+BD=OD+CE=4+1=5,
∴B(5,0);
(2) 如图2,在AM上截取AN=OB,连接FN,
∵A(4,4),
∴OF=AF=4,
在△BOF与△NAF中,
,
∴△BOF≌△NAF(SAS),
∴∠BFO=∠NFA,BF=NF,
∵∠BFM=∠BFO+∠OFM=45°,
∴∠NFA+∠OFM=45°,
∴∠OFA=90°,
∴∠NFM=∠OFA-(∠NFA+∠OFM)
=900-450=45°,
∴∠BFM=∠NFM,
在△BFM与△NFM中,
,
∴△BFM≌△NFM(SAS),
∴BM=NM,
∴AM=AN+NM=OB+BM.
 (1) 如图1,过A作AD⊥x轴,CE⊥x轴,垂足分别为D、E.
(1) 如图1,过A作AD⊥x轴,CE⊥x轴,垂足分别为D、E.∵AD⊥x轴,CE⊥x轴,
∴∠ADB=∠BEC=90°,
∴∠DAB+∠ABD=90°,
∵AB⊥BC,
∴∠EBC+∠ABD=90°,
∴∠DAB=∠EBC,
在△ADB与△BEC中,
|
∴△ADB≌△BEC(AAS),
∴BD=CE,
∵A(4,4),C(1,-1),
∴OD=4,CE=1,

∴OB=OD+BD=OD+CE=4+1=5,
∴B(5,0);
(2) 如图2,在AM上截取AN=OB,连接FN,
∵A(4,4),
∴OF=AF=4,
在△BOF与△NAF中,
|
∴△BOF≌△NAF(SAS),
∴∠BFO=∠NFA,BF=NF,
∵∠BFM=∠BFO+∠OFM=45°,
∴∠NFA+∠OFM=45°,
∴∠OFA=90°,
∴∠NFM=∠OFA-(∠NFA+∠OFM)
=900-450=45°,
∴∠BFM=∠NFM,
在△BFM与△NFM中,
|
∴△BFM≌△NFM(SAS),
∴BM=NM,
∴AM=AN+NM=OB+BM.
看了 在平面直角坐标系中,点A的坐...的网友还看了以下:
如图,点P(3+1,3-1)在双曲线y=kx(x>0)上.(1)求k的值;(2)若正方形ABCD的 2020-05-15 …
椭圆方程公式已知椭圆过(1,3/2)(根号3,负二分之根号三)且中心在原点,焦点在坐标轴上,1求椭 2020-05-16 …
已知函数y=(k-4)x+2-k中,y随x的增大而减小,且图像与y轴的交点落在y轴的副半轴上.(1 2020-06-03 …
已知:平面直角坐标系内有两点A,B,点A(-6,a+3)在x轴上,点B(b-2,5)在y轴上.(1 2020-06-14 …
1.已知一次函数y=(2m+2)x+(3-m).直线与y轴交点在x轴上方,求m的取值范围.2.已知 2020-07-03 …
已知椭圆C1:x平方/100+y平方/64=1,设椭圆C2与椭圆C1的上轴长、短轴长分别相等,且椭 2020-07-09 …
在平面直角坐标系中,点A的坐标是(3a-5,a+1)(1)若点A在y轴上,求a的值及点A的坐标.( 2020-07-26 …
已知抛物线y=x2-px+p2-14(1)若抛物线与y轴交点的坐标为(0,1),求抛物线与x轴交点 2020-07-29 …
如图,在平面直角坐标系中,点A的坐标为(2,3),△ABO的面积是3.图:A在第一象限,O是原点, 2020-08-01 …
1.直线L过点P(3,2),它与直线L1,x+3y-9=0及x轴围成一个等腰三角形(底边在x轴上) 2020-08-02 …