早教吧作业答案频道 -->数学-->
已知:正方形ABCD的边长为4,点E为BC边的中点,点P为AB边上一动点,联结PE,过E作EQ⊥PE交边CD于Q,直线PQ交直线AD于点G.(1)如图,当BP=1.5时,求CQ的长;(2)如图,当点G在射线AD上时,设B
题目详情
已知:正方形ABCD的边长为4,点E为BC边的中点,点P为AB边上一动点,联结PE,过E作EQ⊥PE交边CD于Q,直线PQ交直线AD于点G.
(1)如图,当BP=1.5时,求CQ的长;
(2)如图,当点G在射线AD上时,设BP=x,DG=y,求y关于x的函数关系式,并写出x的取值范围.
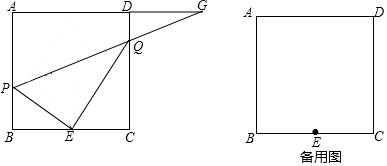
(1)如图,当BP=1.5时,求CQ的长;
(2)如图,当点G在射线AD上时,设BP=x,DG=y,求y关于x的函数关系式,并写出x的取值范围.

▼优质解答
答案和解析
(1)∵点E为BC边的中点,
∴BE=CE=2,
∵EQ⊥PE,
∴∠PEQ=90°,
∴∠PEB+∠QEC=∠EQC+∠QEC=90°,
∴∠PEB=∠EQC,
∵∠B=∠C=90°,
∴△PEB∽△EQC,
∴
=
∴CQ=
,
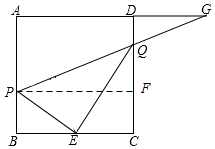
(2)由(1)可知:△PEB∽△EQC,
∴
=
∴CQ=
,
当CQ=4时,
此时x=1,
∴1≤x≤4,
过点P作PF⊥CD于点F,
∴△QPF∽△QGD,
∴
=
∵CF=PB=x,
∴QF=CQ-CF=
-x,
DQ=CD-CQ=4-
∴
=
,
化简可得:y=
(1≤x≤4)
∴BE=CE=2,
∵EQ⊥PE,
∴∠PEQ=90°,
∴∠PEB+∠QEC=∠EQC+∠QEC=90°,
∴∠PEB=∠EQC,
∵∠B=∠C=90°,
∴△PEB∽△EQC,
∴
| PB |
| EC |
| BE |
| CQ |
∴CQ=
| 8 |
| 3 |
(2)由(1)可知:△PEB∽△EQC,
∴
| PB |
| EC |
| BE |
| CQ |

∴CQ=
| 4 |
| x |
当CQ=4时,
此时x=1,
∴1≤x≤4,
过点P作PF⊥CD于点F,
∴△QPF∽△QGD,
∴
| PF |
| DG |
| QF |
| DQ |
∵CF=PB=x,
∴QF=CQ-CF=
| 4 |
| x |
DQ=CD-CQ=4-
| 4 |
| x |
∴
| 4 |
| y |
| ||
4-
|
化简可得:y=
| 4(4x-4) |
| 4-x2 |
看了 已知:正方形ABCD的边长为...的网友还看了以下:
有a、b、c、d、e、f、g七种物质.a为HCl,f的元素质量比为7:3.a能与b、f、d反应,c 2020-05-02 …
在Rt△ABC中,∠ACB=90°,CD⊥AB于D,以CD为半径作⊙C与AE切于E点,过B作BM‖ 2020-06-05 …
根据所学知识,对图中d、e两点生长素浓度的分析合理的是()A.若d点对应的浓度为a,则e点对应c点 2020-07-26 …
如图,已知点A(0,2),直线l:y=-x-2与x轴交于D点,与y轴交于E点,B是直线l上的一个动 2020-07-26 …
如图所示,A、B两点分别是斜面的顶端、底端,C、D是斜面上的两个点,LAC:LCD:LDB=1:3 2020-07-29 …
1.已知集合M={x|x=3n+1,n∈Z}.集合N={x|x=4n+3,n∈Z}.求M∩N2.设 2020-07-30 …
已知椭圆E:x^2/a^2+y^2/b^2=1(a>b>0)的右焦点F(3,0),过点F的直线交椭 2020-07-31 …
已知△ABC中,角C=90度,AB=9,cosA=2/3,把△ABC绕着点C旋转,使得点A落在点D, 2020-11-02 …
如图,AB∥CD,AB=CD,点E、F在直线BC上,且E点在B点的右侧,F点在C点的右侧,BE=CF 2020-11-03 …
已知点F是双曲线C:x^2/a^2-y^2/b^2=1(a>0,b>0)的左焦点P为右支上一点直线P 2021-01-11 …