早教吧作业答案频道 -->数学-->
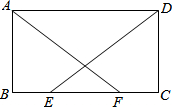
如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.(1)求证:△ABF≌△DCE;(2)若∠BFA=40°,求∠BAF的度数.
题目详情
如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
(1)求证:△ABF≌△DCE;
(2)若∠BFA=40°,求∠BAF的度数.

(1)求证:△ABF≌△DCE;
(2)若∠BFA=40°,求∠BAF的度数.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∵BE=CF,
∴BF=CE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SSS);
(2) ∵△ABF≌△DCE,
∴∠B=∠C,
∵AB∥DC,
∴∠B+∠C=180°,
∴∠B=90°,
∴∠BAF=90°-∠BFA=90°-40°=50°.
∴AB=DC,AB∥DC,
∵BE=CF,
∴BF=CE,
在△ABF和△DCE中,
|
∴△ABF≌△DCE(SSS);
(2) ∵△ABF≌△DCE,
∴∠B=∠C,
∵AB∥DC,
∴∠B+∠C=180°,
∴∠B=90°,
∴∠BAF=90°-∠BFA=90°-40°=50°.
看了 如图,在平行四边形ABCD中...的网友还看了以下:
如图所示,在匀强电场中有边长为2m的等边三角形△ABC,已知电场线的方向平行于△ABC所在平面.已 2020-05-13 …
已知A、B、C、D、E五种物质之间存在以下转化关系。其中A、C两种物质的组成元素相同,且常温下是液 2020-06-09 …
协方差cov(X+20,Y+10)=cov(X,知道了COV(X+a,Y+b)=E[(X+a)(Y 2020-06-17 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
对数函数y=e^x-e^-x/e^x+e^-x转化为用含y的式子表示x的形式.谢咯,对数函数y=e 2020-07-15 …
对数函数y=e^x-e^-x/e^x+e^-x转化为用含y的式子表示x的形式.谢咯,对数函数y=e 2020-07-15 …
f(x),g(x),h(x)在[a,b]上连续,(a,b)上可导,求证存在一个e属于(a,b)使得 2020-07-16 …
高数导数问题.设f(x)=(e^x-e^a)g(x)在x=a处可导,则函数g(x)应该满足条件是? 2020-07-20 …
如图所示,有一半球形容器,其竖直截面为半圆.AB为沿水平方向的直径,D是圆周的最低点,E是AD间某 2020-07-21 …
已知函数f(x)=(a+lnx)除以x(a属于R)若a=4求曲线F(X)在点(e,f(e)处的切线 2020-07-27 …