早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,∠CAB=30°,BC=43cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.(1)求证:△ADO∽△ABC;(2)点P(不与点A重合)是线段AB′上一动点,沿射线AB′的方向以2cm
题目详情
如图,在矩形ABCD中,∠CAB=30°,BC=4
cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.
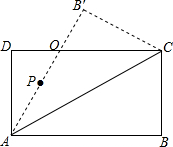
(1)求证:△ADO∽△ABC;
(2)点P(不与点A重合)是线段AB′上一动点,沿射线AB′的方向以2cm/s的速度匀速运动,请你求出△APC的面积S与运动时间t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)中,以AP、B′P、BC的长为边能否构成直角三角形?若能,求出点P的位置;若不能,请说明理由.
| 3 |

(1)求证:△ADO∽△ABC;
(2)点P(不与点A重合)是线段AB′上一动点,沿射线AB′的方向以2cm/s的速度匀速运动,请你求出△APC的面积S与运动时间t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)中,以AP、B′P、BC的长为边能否构成直角三角形?若能,求出点P的位置;若不能,请说明理由.
▼优质解答
答案和解析
(1)在矩形ABCD中,∠ABC=∠ADC=∠BAD=90°,
∵∠CAB=30°,
∴∠CAD=60°,
由折叠得,∠B'AC=∠CAB=30°,
∴∠DAO=∠CAD-∠B'AC=30°=∠BAC,
∵∠ADO=∠ABC=90°,
∴△ADO∽△ABC;
(2)如图,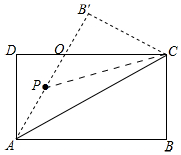 连接PC,
连接PC,
在Rt△ABC中,∠BAC=30°,BC=4
,
∴AB=
BC=12,
由折叠知AB'=AB=12,
由运动知,AP=2t,
由折叠得,B'C=BC=4
cm,
∴S=S△APC=
AP•B'C=
×2t×4
=4
t(0<t≤12);
(3)能构成直角三角形,
由运动知,AP=2t,B'P=AB'-AP=12-2t,
∵以AP、B′P、BC的长为边构成直角三角形,
∴①AP2+B'P2=BC2,
∴(2t)2+(12-2t)2=48,
∴此方程无解;
②AP2+BC2=B'P2,
∴(2t)2+48=(12-2t)2,
∴t=2,
∴AP=2t=4cm,此时,点P在AB'上距点A4cm处
③B'P2+BC2=AP2,(12-2t)2+48=(2t)2,
∴t=4,
∴AP=2t=8cm,此时,点P在AB'上,距点A8cm处.
即:点p距点A是4cm和8cm处时,以AP、B′P、BC的长为边构成直角三角形.
∵∠CAB=30°,
∴∠CAD=60°,
由折叠得,∠B'AC=∠CAB=30°,
∴∠DAO=∠CAD-∠B'AC=30°=∠BAC,
∵∠ADO=∠ABC=90°,
∴△ADO∽△ABC;
(2)如图,
 连接PC,
连接PC,在Rt△ABC中,∠BAC=30°,BC=4
| 3 |
∴AB=
| 3 |
由折叠知AB'=AB=12,
由运动知,AP=2t,
由折叠得,B'C=BC=4
| 3 |
∴S=S△APC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(3)能构成直角三角形,
由运动知,AP=2t,B'P=AB'-AP=12-2t,
∵以AP、B′P、BC的长为边构成直角三角形,
∴①AP2+B'P2=BC2,
∴(2t)2+(12-2t)2=48,
∴此方程无解;
②AP2+BC2=B'P2,
∴(2t)2+48=(12-2t)2,
∴t=2,
∴AP=2t=4cm,此时,点P在AB'上距点A4cm处
③B'P2+BC2=AP2,(12-2t)2+48=(2t)2,
∴t=4,
∴AP=2t=8cm,此时,点P在AB'上,距点A8cm处.
即:点p距点A是4cm和8cm处时,以AP、B′P、BC的长为边构成直角三角形.
看了 如图,在矩形ABCD中,∠C...的网友还看了以下:
如图装置,AB段为倾角为37°的粗糙斜面,动摩擦因数μ1为0.25,BC、CE段光滑,CD为一光滑 2020-04-09 …
已知抛物线y=ax2-2ax+c-1的顶点在直线y=-8/3x+8上,与X轴交于A(-1,0)和B 2020-05-16 …
如图,在矩形ABCD中,AB=4,BC=25/2,O为BC上一点,BO=7/2如图所示,以BC所在 2020-06-12 …
在直角坐标系中,已知点A(0,2),点B(-2,0)过点B和线段OA的中点C作直线BC,以线段BC 2020-06-14 …
哥哥姐姐们谁会这道题啊?帮我解决下呗,谢谢.“要把192.168.1.0段IP划分最少6个子网,应 2020-07-15 …
如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为圆心,OB为半径作半 2020-07-21 …
在如图所示的装置中,平台的AB段粗糙,且长度为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均 2020-07-22 …
已知等腰梯形ABCD中,AD//BC,AD:BC=1:2,点E为边AB中点,点F是边BC上一动点,线 2020-12-07 …
AB和CD是半径为R=1m的0.25半弧形,BC为一段长为2m的水平轨道,质量为2kg的物体从轨道A 2020-12-25 …
在平面直角坐标系中,点A(0,2)点B(-1,0),连接AB,将线段AB绕点逆时针旋转90度得到线段 2020-12-25 …