阅读下面材料：小昊遇到这样一个问题：如图1，在△ABC中，∠ACB=90°，BE是AC边上的中线，点D在BC边上，CD：BD=1：2，AD与BE相交于点P，求APPD的值．小昊发现，过点A作AF∥

Question

阅读下面材料：
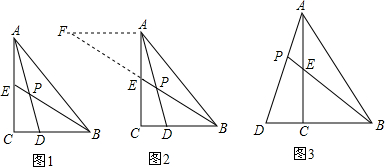
小昊遇到这样一个问题：如图1，在△ABC中，∠ACB=90°，BE是AC边上的中线，点D在BC边上，CD：BD=1：2，AD与BE相交于点P，求 (AP)/(PD)的值．
小昊发现，过点A作AF∥BC，交BE的延长线于点F，通过构造△AEF，经过推理和计算能够使问题得到解决（如图2）．
请回答： (AP)/(PD)的值为___．
参考小昊思考问题的方法，解决问题：
如图 3，在△ABC中，∠ACB=90°，点D在BC的延长线上，AD与AC边上的中线BE的延长线交于点P，DC：BC：AC=1：2：3．
（1）求 (AP)/(PD)的值；
（2）若CD=2，则BP=___．

Answer 1

(AP)/(PD)的值为(3)/(2)．
提示：易证△AEF≌△CEB，则有AF=BC．
设CD=k，则DB=2k，AF=BC=3k，
由AF∥BC可得△APF∽△DPB，
即可得到(AP)/(PD)=(AF)/(BD)=(3)/(2)．
故答案为：(3)/(2)；

解决问题：
（1）过点A作AF∥DB，交BE的延长线于点F，如图，
设DC=k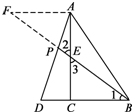，由DC：BC=1：2得BC=2k，DB=DC+BC=3k．
∵E是AC中点，
∴AE=CE．
∵AF∥DB，
∴∠F=∠1．
在△AEF和△CEB中，

∠F=∠1

∠2=∠3

AE=CE

，
∴△AEF≌△CEB，
∴EF=BE，AF=BC=2k．
∵AF∥DB，
∴△AFP∽△DBP，
∴(AP)/(DP)=(FP)/(BP)=(AF)/(DB)=(2k)/(3k)=(2)/(3)．
∴(AP)/(PD)的值为(2)/(3)；

（2）当CD=2时，BC=4，AC=6，
∴EC=(1)/(2)AC=3，EB=√(EC2+BC2)=5，
∴EF=BE=5，BF=10．
∵(FP)/(BP)=(2)/(3)（已证），
∴(BF)/(BP)=(5)/(3)，
∴BP=(3)/(5)BF=(3)/(5)×10=6．
故答案为6．