早教吧作业答案频道 -->数学-->
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)求证:DE⊥FG;(2)连接CG,判断四边形CBFG的形状,并说明理由
题目详情
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.
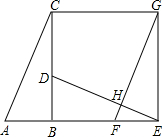
(1)求证:DE⊥FG;
(2)连接CG,判断四边形CBFG的形状,并说明理由.

(1)求证:DE⊥FG;
(2)连接CG,判断四边形CBFG的形状,并说明理由.
▼优质解答
答案和解析
(1)证明:延长ED交AC于M,如图,
∵△ABC绕点B顺时针旋转90°至△DBE,
∴△ABC≌△DBE,
∴∠1=∠2,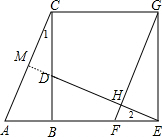
而∠1+∠A=90°,
∴∠2+∠A=90°,
∴∠AME=90°,
∴DE⊥AC,
∵△ABC沿射线平移至△FEG,
∴AC∥FG,
∴DE⊥FG;
(2)四边形CBFG为正方形.理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE,
∴BC=BE,∠CBE=90°,
∵△ABC沿射线平移至△FEG,
∴BC=GE,CG=BE,
∴CB=BE=GE=CG,
而∠CBE=90°,
∴四边形CBFG为正方形.
∵△ABC绕点B顺时针旋转90°至△DBE,
∴△ABC≌△DBE,
∴∠1=∠2,

而∠1+∠A=90°,
∴∠2+∠A=90°,
∴∠AME=90°,
∴DE⊥AC,
∵△ABC沿射线平移至△FEG,
∴AC∥FG,
∴DE⊥FG;
(2)四边形CBFG为正方形.理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE,
∴BC=BE,∠CBE=90°,
∵△ABC沿射线平移至△FEG,
∴BC=GE,CG=BE,
∴CB=BE=GE=CG,
而∠CBE=90°,
∴四边形CBFG为正方形.
看了如图,已知Rt△ABC中,∠A...的网友还看了以下:
如图所示,电源电动势为E、内阻为r,电阻R1=r,电路中的电压表和电流表均为理想电表,闭合开关S, 2020-04-08 …
正方体ABCD-A’B"C"D"中P,Q,R分别是AB,AD,BC的中点,那么正方体的过P,Q,R 2020-05-13 …
同一平面内两圆的半径是R和r,圆心距是d,若以R、r、d为边长,能围成一个三角形,则这两个圆的位置 2020-05-13 …
在边长为r的等边三角形的三个顶点上,各放有等量电荷,电荷均为q.求中心点电势将1c的电荷从无穷远处 2020-05-13 …
在边长为r的等边三角形的三个顶点上,各放有等量电荷,电荷均为q.计算中线交点电势将1c的电荷从无穷 2020-05-13 …
如图为回旋加速器的结构示意图,两个半径为R的D形金属盒相距很近,连接频率为f=Bq4πm的高频交流 2020-05-14 …
A.πA,D(σC=D(R×S))B.πA,R.D(σR.C=S.D(R×S))C.πA,R.D(σ 2020-05-26 …
A.πA,D(σC=D(R×S))B.πA,R.D(σS.C=R.D(R×S))C.πA,R.D(σ 2020-05-26 …
1+r+r^2+...+r^n=[(r^n+1)-1]/r-1如果左边取1+r+r^2,右边[(r 2020-06-02 …
边长为1cm的等边三角形被一个半径为r的圆所覆盖边长为1cm的等边三角形被一个半径为r的圆所覆盖, 2020-06-04 …