早教吧作业答案频道 -->数学-->
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=43AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.(1)当C在B点右
题目详情
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=
AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
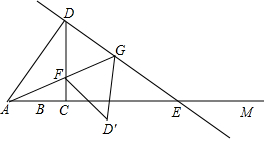
(1)当C在B点右侧时,求AD.DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形;
(3)作点D关于AG的对称点D′,连接FD′,GD′,若四边形DFD′G是平行四边形,求x的值.(直接写出答案)
| 4 |
| 3 |

(1)当C在B点右侧时,求AD.DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形;
(3)作点D关于AG的对称点D′,连接FD′,GD′,若四边形DFD′G是平行四边形,求x的值.(直接写出答案)
▼优质解答
答案和解析
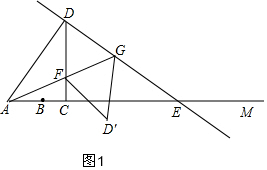 (1)∵CD=
(1)∵CD=
AC,AC=3x,
∴CD=4x,
∵CD⊥AM,
∴∠ACD=90°,
由勾股定理得:AD=5x,
∵AB=6,C在B点右侧,
∴BC=AC-AB=3x-6,
∵BC=FC=3x-6,
∴DF=CD-FC=4x-(3x-6)=x+6;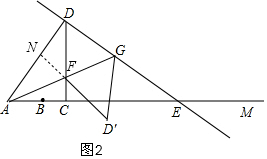
(2)分两种情况:
①当C在B点的右侧时,
∴AC>AB,
∴F必在线段CD上,
∵∠ACD=90°,
∴∠AFD是钝角,若△ADF为等腰三角形,只可能AF=DF,过F作FN⊥AD于N,如图2,
∴AN=ND=2.5x,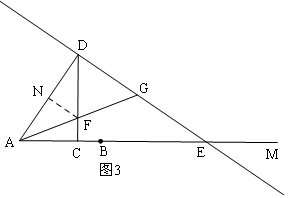
cos∠ADC=
=
,
=
,
x=
;
②当C在线段AB上时,同理可知若△ADF为等腰三角形,只可能AF=DF,
i)当CF<CD时,过F作FN⊥AD于N,如图3,
∵AB=6,AC=3x,
∴BC=CF=6-3x,
∴DF=4x-(6-3x)=7x-6,
cos∠ADC=
=
,
∴
=
,
x=
,
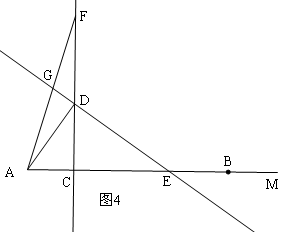
ii)当CF>CD时,如图4,
BC=CF=6-3x,
∴FD=AD=6-3x-4x=6-7x,
则6-7x=5x,
x=
,
综上所述,当x=
或
或
时,△AFD是等腰三角形;
(3)∵四边形DFD′G是平行四边形,且DF=D′F,
∴▱DFD′G是菱形,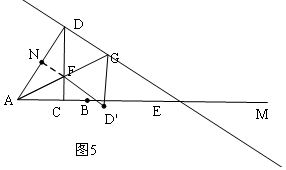
∴DF=DG,
∴∠DFG=∠DGF,
∵∠AFC=∠DFG,
∴∠DGF=∠AFC,
∵∠ACD=∠ADG=90°,
∴∠FAC=∠DAG,
即AF平分∠DAC,
过F作FN⊥AD于N,
当C在AB的延长线上时,如图2,FN=FC=3x-6,DF=x+6,
sin∠CDA=
=
,
解得:x=4,
当C在AB边上时,如图5,FN=FC=6-3x,
DF=7x-6,
sin∠CDA=
=
,
x=
,
综上所述,若四边形DFD′G是平行四边形,x的值是4或
.
 (1)∵CD=
(1)∵CD=| 4 |
| 3 |
∴CD=4x,
∵CD⊥AM,
∴∠ACD=90°,
由勾股定理得:AD=5x,
∵AB=6,C在B点右侧,
∴BC=AC-AB=3x-6,
∵BC=FC=3x-6,
∴DF=CD-FC=4x-(3x-6)=x+6;

(2)分两种情况:
①当C在B点的右侧时,
∴AC>AB,
∴F必在线段CD上,
∵∠ACD=90°,
∴∠AFD是钝角,若△ADF为等腰三角形,只可能AF=DF,过F作FN⊥AD于N,如图2,
∴AN=ND=2.5x,

cos∠ADC=
| DN |
| DF |
| DC |
| AD |
| 2.5x |
| x+6 |
| 4x |
| 5x |
x=
| 48 |
| 17 |
②当C在线段AB上时,同理可知若△ADF为等腰三角形,只可能AF=DF,
i)当CF<CD时,过F作FN⊥AD于N,如图3,
∵AB=6,AC=3x,
∴BC=CF=6-3x,
∴DF=4x-(6-3x)=7x-6,
cos∠ADC=
| DN |
| DF |
| CD |
| AD |

∴
| 2.5x |
| 7x-6 |
| 4x |
| 5x |
x=
| 48 |
| 31 |
ii)当CF>CD时,如图4,
BC=CF=6-3x,
∴FD=AD=6-3x-4x=6-7x,
则6-7x=5x,
x=
| 1 |
| 2 |
综上所述,当x=
| 48 |
| 17 |
| 48 |
| 31 |
| 1 |
| 2 |
(3)∵四边形DFD′G是平行四边形,且DF=D′F,
∴▱DFD′G是菱形,

∴DF=DG,
∴∠DFG=∠DGF,
∵∠AFC=∠DFG,
∴∠DGF=∠AFC,
∵∠ACD=∠ADG=90°,
∴∠FAC=∠DAG,
即AF平分∠DAC,
过F作FN⊥AD于N,
当C在AB的延长线上时,如图2,FN=FC=3x-6,DF=x+6,
sin∠CDA=
| 3x-6 |
| x+6 |
| 3 |
| 5 |
解得:x=4,
当C在AB边上时,如图5,FN=FC=6-3x,
DF=7x-6,
sin∠CDA=
| 6-3x |
| 7x-6 |
| 3 |
| 5 |
x=
| 4 |
| 3 |
综上所述,若四边形DFD′G是平行四边形,x的值是4或
| 4 |
| 3 |
看了如图,射线AM上有一点B,AB...的网友还看了以下:
如图,F为双曲线C:的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原 2020-04-08 …
(本大题满分14分)如图,F为双曲线C:的右焦点。P为双曲线C右支上一点,且位于轴上方,M为左准线 2020-04-08 …
如图,F为双曲线C:x2a2−y2b2=1(a>0,b>0)的右焦点.P为双曲线C右支上一点,且位 2020-04-08 …
如图,F为双曲线C:x2a2−y2b2=1(a>0,b>0)的右焦点,P为双曲线C右支上一点,且位 2020-04-08 …
关于摩擦力受力分析的一个问题______|_A_|_|__B__|------>F由静止启动加速度 2020-05-13 …
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴的距离的差都是1.(1)求曲 2020-05-15 …
已知B1,B2分别是中心在远点,焦点在x轴上椭圆C的上下顶点,F是C的右焦点,FB1=2,F到C的 2020-05-17 …
广大老师同学帮帮忙!如图(图是地面上有A,B在A上,C在B上,水平向左对A施加力F,水平向右对B施加 2020-11-22 …
如图,在等腰直角三角形ABC中,作斜边AB的中垂线,试说明被中垂线分成的的两个三角形也是等腰直角三角 2020-12-25 …
已知点F是双曲线C:x^2/a^2-y^2/b^2=1(a>0,b>0)的左焦点P为右支上一点直线P 2021-01-11 …