正方体ABCD-A1B1C1D1中，M，N，Q分别是棱D1C1，A1D1，BC的中点，点P在对角线BD1上，给出以下命题：①当P在BD1上运动时，恒有MN∥面APC；②若A，P，M三点共线，则BPBD1=23；③若BPBD1=23，则C1Q∥面APC；

Question

正方体ABCD-A₁B₁C₁D₁中，M，N，Q分别是棱D₁C₁，A₁D₁，BC的中点，点P在对角线BD₁上，给出以下命题：
①当P在BD₁上运动时，恒有MN∥面APC；
②若A，P，M三点共线，则

(BP)/(BD1)=(2)/(3)；
③若(BP)/(BD1)=(2)/(3)，则C₁Q∥面APC；
④若过点P且与正方体的十二条棱所成的角都相等的直线有m条；过点P且与直线AB₁和A₁C₁所成的角都为60°的直线有n条，则m+n=7．
其中正确命题的个数为（　　）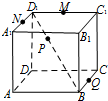

A. 1

B. 2

C. 3

D. 4

Answer 1

①∵M，N，分别是棱D₁C₁，A₁D₁的中点，
∴MN∥A₁C₁∥AC，MN⊄平面APC，AC⊂平面APC，
∴当P在BD₁上运动时，恒有MN∥面APC，正确；
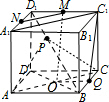
②若A，P，M三点共线，②若A，P，M三点共线，由D₁M∥AB，
∴(D1P)/(BP)=(D1M)/(AB)=(1)/(2)，则(BP)/(BD1)=(2)/(3)，正确；
③若(BP)/(BD1)=(2)/(3)，由②可得：A，P，M三点共线，设对角线BD∩AC=O，连接OM，OQ，则四边形OQC₁M是平行四边形，
∴C₁Q∥OM，
而M点在平面APC内，
∴C₁Q∥平面APC相交，因此正确；
④若过点P且与正方体的十二条棱所成的角都相等的直线有A₁C，D₁B，AC₁，DB₁，4条．
连接B₁C，A₁C₁∥AC，由正方体的性质可得△AB₁C是等边三角形，则点P取点D₁，则直线AD₁，CD₁满足条件，
∴过点P且与直线AB₁和A₁C₁所成的角都为60°的直线有且只有2条，过P且与直线AB₁和A₁C₁所成的角都为60°的直线有n条，则m+n=6条，因此不正确．
其中正确命题为①②③，其个数为3．
故选：C．