早教吧作业答案频道 -->数学-->
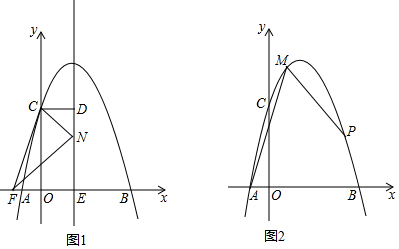
二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(-1,0)、B(4,0)(1)求此二次函数的表达式(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(-76,0),动
题目详情
二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(-1,0)、B(4,0)
(1)求此二次函数的表达式
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(-
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标.
(1)求此二次函数的表达式
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(-
| 7 |
| 6 |
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标.

▼优质解答
答案和解析
(1)当x=0时,y=4,
∴C(0,4).
设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入得:-4a=4,解得a=-1,
∴抛物线的解析式为y=-x2+3x+4.
(2)x=-
=
.
∴CD=
,EF=
.
设点N的坐标为(0,a)则ND=4-a,NE=a.
当△CDN∽△FEN时,
=
,即
=
,解得a=
,
∴点N的坐标为(0,
).
当△CDN∽△NEF时,
=
,即
=
,解得:a=2.
∴点N的坐标为(0,2).
综上所述,点N的坐标为(0,
)或(0,2).
(3)如图所示:过点A作AD∥y轴,过点M作DM∥x轴,交点为D,过点A作AE⊥AM,取AE=AM,作EF⊥x轴,垂足为F,连结EM交抛物线与点P.
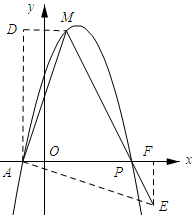
∵AM=AE,∠MAE=90°,
∴∠AMP=45°.
将x=1代入抛物线的解析式得:y=6,
∴点M的坐标为(1,6).
∴MD=2,AD=6.
∵∠DAM+∠MAF=90°,∠MAF+∠FAE=90°,
∴∠DAM=∠FAE.
在△ADM和△AFE中,
,
∴△ADM≌△AFE.
∴EF=DM=2,AF=AD=6.
∴E(5,-2).
设EM的解析式为y=kx+b.
将点M和点E的坐标代入得:
,解得k=-2,b=8,
∴直线EM的解析式为y=-2x+8.
将y=-2x+8与y=-x2+3x+4联立,解得:x=1或x=4.
将x=4代入y=-2x+8得:y=0.
∴点P的坐标为(4,0).
∴C(0,4).
设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入得:-4a=4,解得a=-1,
∴抛物线的解析式为y=-x2+3x+4.
(2)x=-
| b |
| 2a |
| 3 |
| 2 |
∴CD=
| 3 |
| 2 |
| 8 |
| 3 |
设点N的坐标为(0,a)则ND=4-a,NE=a.
当△CDN∽△FEN时,
| EM |
| DN |
| EF |
| CD |
| a |
| 4-a |
| ′16 |
| 9 |
| 64 |
| 25 |
∴点N的坐标为(0,
| 64 |
| 25 |
当△CDN∽△NEF时,
| CD |
| NE |
| DN |
| EF |
| ||
| a |
| 4-a | ||
|
∴点N的坐标为(0,2).
综上所述,点N的坐标为(0,
| 64 |
| 25 |
(3)如图所示:过点A作AD∥y轴,过点M作DM∥x轴,交点为D,过点A作AE⊥AM,取AE=AM,作EF⊥x轴,垂足为F,连结EM交抛物线与点P.

∵AM=AE,∠MAE=90°,
∴∠AMP=45°.
将x=1代入抛物线的解析式得:y=6,
∴点M的坐标为(1,6).
∴MD=2,AD=6.
∵∠DAM+∠MAF=90°,∠MAF+∠FAE=90°,
∴∠DAM=∠FAE.
在△ADM和△AFE中,
|
∴△ADM≌△AFE.
∴EF=DM=2,AF=AD=6.
∴E(5,-2).
设EM的解析式为y=kx+b.
将点M和点E的坐标代入得:
|
∴直线EM的解析式为y=-2x+8.
将y=-2x+8与y=-x2+3x+4联立,解得:x=1或x=4.
将x=4代入y=-2x+8得:y=0.
∴点P的坐标为(4,0).
看了二次函数y=ax2+bx+4的...的网友还看了以下:
下列说法:(1)绝对值最小的实数不存在;(2)实数与数轴上的点一一对应点;(3)平方根等于本身的数 2020-05-02 …
一次函数与y轴相交,得锐角,锐角与k的关系.一次函数y=-kx+b(k≠0一次函数与y轴相交,得锐 2020-05-14 …
现有一副直角三角板(角度分别为30°、60°、90°和45°、45°、90°),如图(1),其中一 2020-06-22 …
如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若 2020-07-10 …
(本小题满分12分)设函数若它是R上的单调函数,且1是它的零点。(1)求实数a的值;(2)设的图象 2020-07-21 …
初二的勾股定理如图,已知在数轴上点A表示数1,AB与数轴垂直,AB=2,连结OB,以O为圆心,OB 2020-07-26 …
如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚 2020-07-30 …
如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置①开始,在无滑动的情况下沿数轴向右翻滚 2020-07-30 …
如图,已知直线Y=-1/2+m分别与x、y轴交与点C、D,与反比例函数y=6/x的图像在第一象限内 2020-08-03 …
(2006•南宁)如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为 2020-11-13 …