早教吧作业答案频道 -->数学-->
如图①,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,求证:MN=AM+CN.如图②,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上.若∠MBN=12∠ABC,试探究线段MN、AM、CN有怎样的数量
题目详情
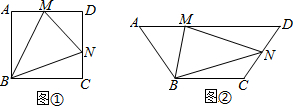
如图①,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,求证:MN=AM+CN.
如图②,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上.若∠MBN=
∠ABC,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想并给予证明.
如图②,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上.若∠MBN=
| 1 |
| 2 |

▼优质解答
答案和解析
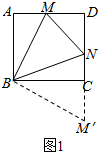 (1)证明:如图1,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
(1)证明:如图1,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,
∵∠MBN=45°=
∠ABC,
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=
∠ABC=45°,
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN;
(2) MN=AM+CN.
理由如下:
如图2,∵BC∥AD,AB=BC=CD,
∴梯形ABCD是等腰梯形,
∴∠A+∠BCD=180°,
把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,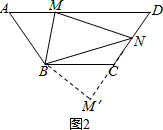
∵∠MBN=
∠ABC,
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=
∠ABC,
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN.
 (1)证明:如图1,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
(1)证明:如图1,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,
∵∠MBN=45°=
| 1 |
| 2 |
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=
| 1 |
| 2 |
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵
|
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN;
(2) MN=AM+CN.
理由如下:
如图2,∵BC∥AD,AB=BC=CD,
∴梯形ABCD是等腰梯形,
∴∠A+∠BCD=180°,
把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,

∵∠MBN=
| 1 |
| 2 |
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=
| 1 |
| 2 |
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵
|
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN.
看了如图①,在正方形ABCD中,点...的网友还看了以下:
关于下列图解的理解正确的是()A.基因自由组合定律的实质表现在图中的⑥B.③⑥过程表示减数分裂过程 2020-04-11 …
读图,回答问题.(1)写出A、B点的地理坐标.A,B.(2)用红笔在图中标出东西半球的分界线和赤道 2020-04-23 …
读图,回答问题.(1)写出A、B点的地理坐标.A,B.(2)用红笔在图中标出东西半球的分界线和赤道 2020-04-24 …
读下图,据此回答1-3题:1.四幅图中位在亚洲与北美洲边界的图是:A.a图B.b图C.c图D.d图 2020-05-02 …
如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点C与点A重合,请在图中 2020-05-16 …
如图所示,点C在线段BE上,在BE同侧作等边△ABC和等边△DCE,那么,从旋转的角度我们可以看到 2020-06-20 …
如图,在△ABC中,AB=AC,AM是外角∠DAC的平分线.(1)实践与操作:尺规作图,并在图中标 2020-06-22 …
如图所示,图甲中瓶子的底部垫一层细沙的好处是什么?图乙中点燃棉花的作用是什么?图丙中会产生什么现象 2020-07-11 …
已知线段AB=4,点C是平面上一点(不与A,B重合),M、N分别是线段CA,CB的中点.(1)当C 2020-07-20 …
在正方形网格中有ABC三个点.(1)在图甲中找到格点D,使得以A、B、C、D四点组成的凸四边形为轴 2020-07-25 …