早教吧作业答案频道 -->数学-->
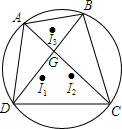
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
题目详情
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.

▼优质解答
答案和解析
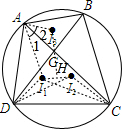 证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,
证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,
延长I3G交I1I2于点H,
∵I1、I2、I3分别为△ADC、△BDC、△ABG的内心,
∴∠AI3G=90°+
∠ABD,∠AI1C=90°+
∠ADC,
∴∠DI1C=90°+
∠DAC,∴∠DI2C=90°+
∠DBC,
∠1+∠2=
(∠DAC+∠BAC),
又∵∠DAC=∠DBC,
∴∠DI1C=∠DI2C,
∴点D、I1、I2、C四点共圆,
∴∠I2I1C=∠I2DC=
∠BDC=
∠BAC,
∴∠I3HI1=360°-(∠1+∠2+∠AI3G+∠AI1H)
∵∠1+∠2+∠AI3G+∠AI1H=
(∠DAC+∠BAC)+90°+
∠ABD+90°+
∠ADC-I2I1C
=180°+
(∠DAC+∠BAC+∠ABD+∠ADC+∠BAC)
=180°+
(∠ABD+∠DBC+∠ADC)
=270°,
∴∠I3HI1=360°-270°=90°,
∴I3G⊥I1I2.
 证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,
证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,延长I3G交I1I2于点H,
∵I1、I2、I3分别为△ADC、△BDC、△ABG的内心,
∴∠AI3G=90°+
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DI1C=90°+
| 1 |
| 2 |
| 1 |
| 2 |
∠1+∠2=
| 1 |
| 2 |
又∵∠DAC=∠DBC,
∴∠DI1C=∠DI2C,
∴点D、I1、I2、C四点共圆,
∴∠I2I1C=∠I2DC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠I3HI1=360°-(∠1+∠2+∠AI3G+∠AI1H)
∵∠1+∠2+∠AI3G+∠AI1H=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=180°+
| 1 |
| 2 |
=180°+
| 1 |
| 2 |
=270°,
∴∠I3HI1=360°-270°=90°,
∴I3G⊥I1I2.
看了如图,四边形ABCD内接于圆,...的网友还看了以下:
在下列化学平衡体系中,若增大压强,平衡向正反应方向移动的是A:2HL(g)H2(g)+L2(g)B 2020-05-14 …
mathematica解一元六次方程Solve[{b==f+a,c+d==b,f+g==d,40- 2020-05-16 …
体积相同但材料不同的甲、乙、丙三个小球,放在同一液体中静止后的位置,如图所示,三个小球所受重力间的 2020-06-16 …
∫g(f(x))dx=∫g(x)d什么把前面的什么拉到d后面?我不记得是∫g(x)f(x)dx还是 2020-06-23 …
在容积为1L的密闭容器中,加入1.0molA和2.2molB进行如下反应:A(g)+2B(g)C( 2020-07-12 …
python组合问题有一个二维数列list=[['a','b'],['c','d','e'],'f 2020-07-17 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.( 2020-07-19 …
(x-3)6=ax6+bx5+cx4+dx3+ex2+fx+g(其中数字为x的次数)求a+b+c+ 2020-07-30 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.(e 2020-11-19 …
1、已知二叉树的前序遍历序列和中序遍历序列分别是:B,A,C,D,F,E,G和D,C,A,F,G,E 2020-12-05 …