早教吧作业答案频道 -->数学-->
函数f(x)=-x3+3x2-ax-2a,若存在唯一的正整数x0,使得f(x0)>0,则a的取值范围是.
题目详情
函数f(x)=-x3+3x2-ax-2a,若存在唯一的正整数x0,使得f(x0)>0,则a的取值范围是___.
▼优质解答
答案和解析
由题意设g(x)=-x3+3x2,h(x)=a(x+2),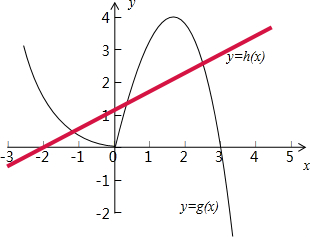
则g′(x)=-3x2+6x=-3x(x-2),
所以g(x)在(-∞,0)、(2,+∞)上递减,在(0,2)上递增,
且g(0)=g(3)=0,g(2)=-23+3•22=4,
在一个坐标系中画出两个函数图象如图:
因为存在唯一的正整数x0,使得f(x0)>0,
即g(x0)>h(x0),
所以由图得x0=2,则
,即
,
解得23≤a<1,
所以a的取值范围是[
,1),
故答案为:[
,1).

则g′(x)=-3x2+6x=-3x(x-2),
所以g(x)在(-∞,0)、(2,+∞)上递减,在(0,2)上递增,
且g(0)=g(3)=0,g(2)=-23+3•22=4,
在一个坐标系中画出两个函数图象如图:
因为存在唯一的正整数x0,使得f(x0)>0,
即g(x0)>h(x0),
所以由图得x0=2,则
|
|
解得23≤a<1,
所以a的取值范围是[
| 2 |
| 3 |
故答案为:[
| 2 |
| 3 |
看了函数f(x)=-x3+3x2-...的网友还看了以下:
函数y=32−3x2的单调递减区间是. 2020-04-25 …
函数f(x)=-x3+3x2-2的凹区间是. 2020-05-13 …
二次函数y=3x2-6x+5的图象的顶点坐标是. 2020-05-13 …
二次函数y=-3x2-6x+5的图象的顶点坐标是. 2020-05-13 …
物体做匀加速直线运动,在时间T内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则物体 2020-05-17 …
已知样本x1,x2,x3的方差是2,则样本3x1,3x2,3x3的方差是. 2020-06-10 …
已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为. 2020-06-30 …
抗利尿激素(ADH)是9肽,可作用于肾小管,激活肾小管细胞内一系列反应,促进水通道蛋白-2插入肾小 2020-07-01 …
我们称顶点相同的两条抛物线为同位抛物线,已知抛物线C1:y=2x2-4x+3.(1)下列抛物线中, 2020-07-09 …
用一把刻度尺测量某物体的长度,记录到的数据是5.72cm和5.73cm,则准确值是cm,所用的刻度 2020-07-17 …