早教吧作业答案频道 -->数学-->
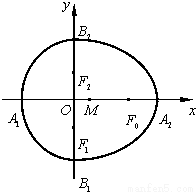
附加题:已知半椭圆与半椭圆组成的曲线称为“果圆”,其中a2=b2+c2,a>b>c>0,F、F1、F2是对应的焦点.(1)(文)若三角形FF1F2是边长为1的等边三角形,求“果圆
题目详情
附加题:已知半椭圆 与半椭圆
与半椭圆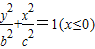 组成的曲线称为“果圆”,其中a 2 =b 2 +c 2 ,a>b>c>0,F 、F 1 、F 2 是对应的焦点.
组成的曲线称为“果圆”,其中a 2 =b 2 +c 2 ,a>b>c>0,F 、F 1 、F 2 是对应的焦点.
(1)(文)若三角形F F 1 F 2 是边长为1的等边三角形,求“果圆”的方程.
(2)(理)当|A 1 A 2 |>|B 1 B 2 |时,求 的取值范围.
的取值范围.
 与半椭圆
与半椭圆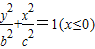 组成的曲线称为“果圆”,其中a 2 =b 2 +c 2 ,a>b>c>0,F 、F 1 、F 2 是对应的焦点.
组成的曲线称为“果圆”,其中a 2 =b 2 +c 2 ,a>b>c>0,F 、F 1 、F 2 是对应的焦点.(1)(文)若三角形F F 1 F 2 是边长为1的等边三角形,求“果圆”的方程.
(2)(理)当|A 1 A 2 |>|B 1 B 2 |时,求
 的取值范围.
的取值范围.
▼优质解答
答案和解析
分析:
(1)由三角形FF1F2是边长为1的等边三角形,得出a,b,c的关系,求出a,b,c的值,进而得出“果圆”的方程.(2)由|A1A2|>|B1B2|可得a,b,c的二次齐次式,把c用a,b代替,得a,b的二次齐次式,可求出的取值范围.
(1)∵F(c,0),,∴,,于是,,所求“果圆”方程为(x≥0)和(x≤0).(2)由题意,得a+c>2b,c>2b-a,即.两边平方得a2-b2>(2b-a)2,得,又b>c,b,∴b2>c2,b2>a2-b2,∴.∴.
点评:
本题考查如何把新定义转化成我们熟悉的内容,做题时留心观察,找准突破口.
分析:
(1)由三角形FF1F2是边长为1的等边三角形,得出a,b,c的关系,求出a,b,c的值,进而得出“果圆”的方程.(2)由|A1A2|>|B1B2|可得a,b,c的二次齐次式,把c用a,b代替,得a,b的二次齐次式,可求出的取值范围.
(1)∵F(c,0),,∴,,于是,,所求“果圆”方程为(x≥0)和(x≤0).(2)由题意,得a+c>2b,c>2b-a,即.两边平方得a2-b2>(2b-a)2,得,又b>c,b,∴b2>c2,b2>a2-b2,∴.∴.
点评:
本题考查如何把新定义转化成我们熟悉的内容,做题时留心观察,找准突破口.
看了附加题:已知半椭圆与半椭圆组成...的网友还看了以下:
高中数学,几何急!已知椭圆G:x^2/a^2+y^2/b^2=1(a>b>0)的离心率为1/2过椭 2020-05-14 …
如图,已知P是椭圆x2a2+y2b2=1(a>b>0)上且位于第一象限的一点,F是椭圆的右焦点,O 2020-05-15 …
椭圆求圆心已知一个椭圆方程,求圆心坐标.(x-x0)^2/a^2+(y-y0)^2/b^2=1已知 2020-05-21 …
如何证明被椭圆截得的直线的线段的中点在同一直线上已知一个椭圆x平方/4+y平方/9=1,一组平行直 2020-06-03 …
如图,椭圆与椭圆中心在原点,焦点均在轴上,且离心率相同.椭圆的长轴长为,且椭圆的左准线被椭圆截得的 2020-06-21 …
已知点是椭圆:的一个顶点,椭圆的离心率为.(1)求椭圆的方程;(2)已知点是定点,直线:交椭圆于不 2020-06-21 …
关于椭圆的标准方程.要具体过程.1.已知P为椭圆C上一点,F1,F2为椭圆的焦点,且绝对值F1F2 2020-06-21 …
已知P为椭圆上一点已知P为椭圆x^2/a^2+y^2/b^2=1(a>b>0)上一点,F1,F2为 2020-06-30 …
已知P是椭圆x^2/4y^2/3=1上的一点,F1,F2是该椭圆的两个焦点,若三角形PF1F2的内 2020-07-20 …
已知椭圆C:(a>b>0)则称以原点为圆心,r=的圆为椭圆C的“知己圆”。(Ⅰ)若椭圆过点(01), 2020-11-27 …