早教吧作业答案频道 -->数学-->
已知直线AB分别交x,y输于A(4,0),B两点,C(-4,a)为直线y=-x与直线AB的公共点.(1)求点B的坐标;(2)已知动点M在直线y=x+6上,是否存在点M,使得S△OMB=S△OMA,若存在,求出点M的坐
题目详情
已知直线AB分别交x,y输于A(4,0),B两点,C(-4,a)为直线y=-x与直线AB的公共点.
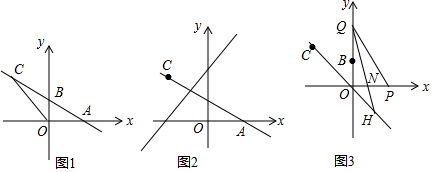
(1)求点B的坐标;
(2)已知动点M在直线y=x+6上,是否存在点M,使得S△OMB=S△OMA,若存在,求出点M的坐标,若不存在,说明理由;
(3)点P,Q分别是x轴,y轴正半轴上一动点,Q在点B上方,且OP=BQ,QH是∠OQP的角平分线,交直线CD于H,求PQ-
OH的值.

(1)求点B的坐标;
(2)已知动点M在直线y=x+6上,是否存在点M,使得S△OMB=S△OMA,若存在,求出点M的坐标,若不存在,说明理由;
(3)点P,Q分别是x轴,y轴正半轴上一动点,Q在点B上方,且OP=BQ,QH是∠OQP的角平分线,交直线CD于H,求PQ-
| 2 |
▼优质解答
答案和解析
(1)∵点C(-4,a)为直线y=-x上一点,
∴a=-1×(-4)=4,
∴点C(-4,4).
设直线AB的解析式为y=kx+b,
将A、C坐标分别代入直线AB的解析式得:
,
解得:
,
∴直线AB的解析式为y=-
x+2,
令x=0时,y=2,
∴点B的坐标为(0,2).
(2)假设存在,设点M的坐标为(m,m+6).
∵点A(4,0)、点B(0,2)、点M(m,m+6),
∴OA=4,OB=2,|Mx|=|m|,|My|=|m+6|,
∴S△OMA=
OA•|My|=2|m+6|;
S△OMB=
OB•|Mx|=|m|.
∵S△OMB=S△OMA,
∴2|m+6|=|m|,
∴2(m+6)=m或2(m+6)=-m,
解得:m1=-12,m2=-4.
∵-12+6=-6,-4+6=2,
∴M点的坐标为(-12,-6)或(-4,2).
故动点M在直线y=x+6上,存在点M使得S△OMB=S△OMA,点M的坐标为(-12,-6)或(-4,2).
(3)设点H(t,-t),P(a,0),QH与x轴的交点为M,如图所示,作HN⊥y轴于N,HF⊥PQ于F,HM⊥x轴于M.
则HN=HM=HF.△QHN≌△QHF,四边形OMHN是正方形,边长为t,
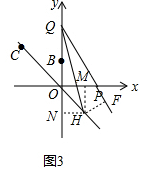
∴QN=QF,
∴2+a+t=PQ+(a-t),
∴PQ-2t=2,∵OH=
t,
∴
OH=2t,
∴PQ-
t=2.
∴a=-1×(-4)=4,
∴点C(-4,4).
设直线AB的解析式为y=kx+b,
将A、C坐标分别代入直线AB的解析式得:
|
解得:
|
∴直线AB的解析式为y=-
| 1 |
| 2 |
令x=0时,y=2,
∴点B的坐标为(0,2).
(2)假设存在,设点M的坐标为(m,m+6).
∵点A(4,0)、点B(0,2)、点M(m,m+6),
∴OA=4,OB=2,|Mx|=|m|,|My|=|m+6|,
∴S△OMA=
| 1 |
| 2 |
S△OMB=
| 1 |
| 2 |
∵S△OMB=S△OMA,
∴2|m+6|=|m|,
∴2(m+6)=m或2(m+6)=-m,
解得:m1=-12,m2=-4.
∵-12+6=-6,-4+6=2,
∴M点的坐标为(-12,-6)或(-4,2).
故动点M在直线y=x+6上,存在点M使得S△OMB=S△OMA,点M的坐标为(-12,-6)或(-4,2).
(3)设点H(t,-t),P(a,0),QH与x轴的交点为M,如图所示,作HN⊥y轴于N,HF⊥PQ于F,HM⊥x轴于M.
则HN=HM=HF.△QHN≌△QHF,四边形OMHN是正方形,边长为t,

∴QN=QF,
∴2+a+t=PQ+(a-t),
∴PQ-2t=2,∵OH=
| 2 |
∴
| 2 |
∴PQ-
| 2 |
看了已知直线AB分别交x,y输于A...的网友还看了以下:
直线X2y-5的方向向量d怎么算.恩.求..直线是X+2Y-5=0.答案是(-2,1)怎么得来的 2020-03-31 …
(2011•江苏模拟)空间存在一沿x轴方向的静电场,电场强度E随x变化的关系如图所示,图线关于坐标 2020-05-13 …
如图,从直径是x+2y的圆中挖去一个直径为x的圆和两个直径为y的圆,则剩余部分的面积是πxy+12 2020-05-14 …
若b>0,则x的绝对值>b是x>b的什么条件 2020-06-03 …
一元二次方程题难...已知a.b是x^2-7x+8=0的两根a>b不解方程求(2/a)+3b^2= 2020-06-10 …
大一的有关极限的问题,就比方说limX趋于1但是如果后面的式子是1/1-x或者2/1-x^2分母趋 2020-06-11 …
在平面直角坐标系中,我们把横,纵坐标都是整数的点叫做整点.已知点{04},点B是X轴正半轴上的整点 2020-06-11 …
如图是反比例函数y=9/x的图像,点c的坐标为(0,2),若点a是函数y=9/x图像上一点,点b是 2020-06-14 …
若平面向量a=(3,x),b=(4,-3),且a垂直b,则x的值等于?谁会说下哈#17 2020-06-15 …
设X是包含10个元素的集合,A,B是X中的两个互不相交的子集,分别含有3,4个元素,则X中既不包含 2020-06-18 …