早教吧作业答案频道 -->数学-->
已知一次函数y1=k1x+b与反比例函数y2=k2x相交于点A、B,与y轴交于点C,与x轴交于点D,过点A作AE⊥x轴于点E,点O为DE中点,连接CE,已知S△ADE=4,tan∠DCO=12.(1)求y1和y2的解析式;(2)将△ACE
题目详情
已知一次函数y1=k1x+b与反比例函数y2=
相交于点A、B,与y轴交于点C,与x轴交于点D,过点A作AE⊥x轴于点E,点O为DE中点,连接CE,已知S△ADE=4,tan∠DCO=
.
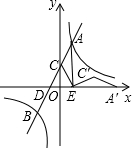
(1)求y1和y2的解析式;
(2)将△ACE绕着点E顺时针旋转90°得△A'C'E,连接AA'、BA',求△AA'B的面积.
| k2 |
| x |
| 1 |
| 2 |

(1)求y1和y2的解析式;
(2)将△ACE绕着点E顺时针旋转90°得△A'C'E,连接AA'、BA',求△AA'B的面积.
▼优质解答
答案和解析
(1)∵O是DE的中点,CO∥AE,
∴CO是△ADE的中位线,
∴AE=2CO,
设CO=m,
∴AE=2m,
∵tan∠DCO=
,
∴
=
,
∴DO=
m,
∴DE=m,
∵S△ADE=4,
∴
DE•AE=4,
∴m2=4,
∴m=2,
∴C(0,2),A(1,4),
将点A(1,4)代入y2=
,
∴k2=4,
将A(1,4)和C(0,2)代入y1=k1x+b,
∴
,
∴解得
,
∴y1=2x+2,y2=
,
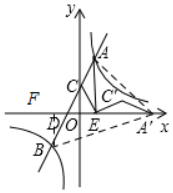
(2)过点B作BF⊥x轴于点F,
联立
,
解得:x=-2或x=1,
∴B(-2,-2),
∴BF=2,
令y=0代入y1=2x+2,
∴D(-1,0),
由题意可知:A′E=AE=4,
∴A′D=OD+OE+AE=6,
∴△AA'B的面积为:
A′D•BF+
A′D•AE=18,
∴CO是△ADE的中位线,
∴AE=2CO,
设CO=m,
∴AE=2m,
∵tan∠DCO=
| 1 |
| 2 |
∴
| DO |
| CO |
| 1 |
| 2 |
∴DO=
| 1 |
| 2 |
∴DE=m,
∵S△ADE=4,
∴
| 1 |
| 2 |
∴m2=4,
∴m=2,
∴C(0,2),A(1,4),
将点A(1,4)代入y2=
| k2 |
| x |
∴k2=4,
将A(1,4)和C(0,2)代入y1=k1x+b,
∴
|
∴解得
|

∴y1=2x+2,y2=
| 4 |
| x |
(2)过点B作BF⊥x轴于点F,
联立
|
解得:x=-2或x=1,
∴B(-2,-2),
∴BF=2,
令y=0代入y1=2x+2,
∴D(-1,0),
由题意可知:A′E=AE=4,
∴A′D=OD+OE+AE=6,
∴△AA'B的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
看了已知一次函数y1=k1x+b与...的网友还看了以下:
l1:y=k1x+b1和直线l2:y=k2+b2l1:y=k1x+b1和直线l2:y=k2+b2当 2020-06-03 …
(2013•连云港)如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=k1x的图 2020-06-13 …
如图所示,正比例函数y=k1x的图象与反比例函数y=k2/x的图象交于A,B两点,点A的坐标如图所 2020-06-14 …
数学分析里实数部分一个命题的问题.关于不足近似和过剩近似谢谢!还有那个命题X=A0.A1A2A3. 2020-07-09 …
(a,b)关于y=x+m的对称点()(a,b)关于y=-x+n的对称点() 2020-07-23 …
如图,已知直线y=k1x+b与x轴,y轴相交于P,Q两点,则y=k2x的图象相交于A(-2,m), 2020-07-29 …
已知反比例函数y=k1x与y=k2x,P(t,0)是x轴上的一个动点,过P作x轴的垂线分别交函数y 2020-08-03 …
(2010•永嘉县二模)如图,两个反比例函数y=k1x和y=k2x(其中k1>0>k2)在第一象限内 2020-12-22 …
比如x=0.333325...y=0.333312...明显x>y,但书本上说,假如x>y,则有:x 2020-12-27 …
一次函数y=k1x+b和反比例函数y=k2/x的图像相交与P(n-1,n+1).点Q(0,a)在函数 2021-02-01 …