问题探究：（1）已知：如图1，在正方形ABCD中，点E、H分别在BC、AB上，若AE⊥DH于点O，求证AE=DH；类比探究：（2）如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，

Question

问题探究：
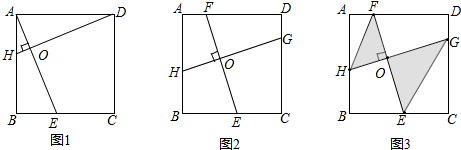
（1）已知：如图1，在正方形ABCD中，点E、H分别在BC、AB上，若AE⊥DH于点O，求证AE=DH；
类比探究：
（2）如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，探究线段EF与HG的数量关系，并说明理由；
拓展应用：
（3）已知，如图3，在（2）问条件下，若BC=4，E为BC的中点，AF=(1)/(4)AD，求HG的长

Answer 1

（1）证明：∵四边形ABCD是正方形，
∴AB=DA，∠ABE=90°=∠DAH．
∴∠HAO+∠OAD=90°．
∵AE⊥DH，
∴∠ADO+∠OAD=90°．
∴∠HAO=∠ADO，
在△ABE和△DAH中

∠HAO=∠DAH

AB=AD

∠B=∠HAD

，
∴△ABE≌△DAH（ASA），
∴AE=DH．

（2） EF=GH．
理由：如图2，将FE平移到AM处，则AM∥EF，AM=EF．
将GH平移到DN处，则DN∥GH，DN=GH．

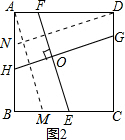
∵EF⊥GH，
∴AM⊥DN，
根据（1）的结论得AM=DN，
所以EF=GH；

（3） 如图3，

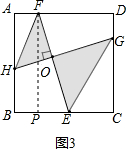
过点F作FP⊥BC于点P，
∵四边形ABCD是正方形，BC=4，
∴AD=BC=AB=FP=4，
∵E为BC的中点，AF=(1)/(4)AD，
∴BE=2，AF=1，
∴PE=2-1=1，
在Rt△FPE中，EF=√(42+12)=√(17)，
由（2）得：HG=EF，
∴HG=√(17)．