早教吧作业答案频道 -->数学-->
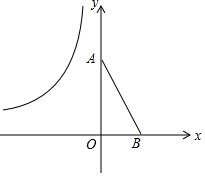
如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线y=-6x(x<0)上,则旋转中心P的坐标为
题目详情
如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线y=
(x<0)上,则旋转中心P的坐标为___.
| -6 |
| x |

▼优质解答
答案和解析
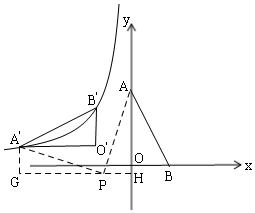 由旋转得:△AOB≌△A′O′B′,
由旋转得:△AOB≌△A′O′B′,
∴A′O′=AO=4,O′B′=OB=2,
设A′(m,-
),则B′(m+4,-
+2),
则(m+4)(-
+2)=-6,
m2+4m-12=0,
(m+6)(m-2)=0,
m1=-6,m2=2(舍),
∴A′(-6,1),B′(-2,3),
过P作GH∥x轴,交y轴于H,过A′作A′G⊥x轴,连接PA、PA′,
设P(x,y),
则A′G=1-y,PG=6+x,PH=-x,AH=4-y,
由旋转得:AP=A′P,
易证明△PA′G≌△APH,
∴A′G=PH,PG=AH,
则
,
解得:
,
∴P(-
,-
);
故答案为:(-
,-
).
 由旋转得:△AOB≌△A′O′B′,
由旋转得:△AOB≌△A′O′B′,∴A′O′=AO=4,O′B′=OB=2,
设A′(m,-
| 6 |
| m |
| 6 |
| m |
则(m+4)(-
| 6 |
| m |
m2+4m-12=0,
(m+6)(m-2)=0,
m1=-6,m2=2(舍),
∴A′(-6,1),B′(-2,3),
过P作GH∥x轴,交y轴于H,过A′作A′G⊥x轴,连接PA、PA′,
设P(x,y),
则A′G=1-y,PG=6+x,PH=-x,AH=4-y,
由旋转得:AP=A′P,
易证明△PA′G≌△APH,
∴A′G=PH,PG=AH,
则
|
解得:
|
∴P(-
| 3 |
| 2 |
| 1 |
| 2 |
故答案为:(-
| 3 |
| 2 |
| 1 |
| 2 |
看了如图,已知原点O,A(0,4)...的网友还看了以下:
如图,O为∠PAQ的角平分线上的一点,OB垂直AP于点B,以O为圆心,OB为半径做圆O,求证AQ与圆 2020-03-31 …
如图,O为矩形ABCD的对称中心,将直角三角板的直角顶点与O点重合,转动三角板,使三角板的两直角边 2020-05-15 …
如图,⊙O为正△ABC的内切圆,四边形EFGH为⊙O的内接正方形,且EF=根号2,求正三角形. 2020-05-16 …
接着上面 如图,O为码头,A,B两个灯塔与码头的距离相等,OA,OB为海岸线,一轮船从码头开出,计 2020-05-16 …
如图,O为角PAQ的角平分线上的一点,OB垂直AB于B,以O为圆心OB为半径作圆O.求证 2020-05-20 …
图①,O为坐标原点,x轴正半轴上的B点时,四边形是平行四边形OACB,罪∠AOB=4/5,反函数Y 2020-06-14 …
如图,O为坐标原点,A(6,m)是双曲线y=12/x上的一点,过点A做直线y=x的垂线,交双曲线与 2020-06-14 …
如图,O为坐标原点,点A,B,C均在⊙O上,点A在第一象限,点C(1,0),设∠COA=θ(1)若 2020-08-02 …
如图,O为△ABC内一点,∠A=80°,∠CBO=1/m∠CBA,∠BCO=1/m∠BCA(1)若m 2020-12-25 …
如图,O为△ABC内一点,∠A=80°,∠CBO=1/m∠CBA,∠BCO=1/m;;∠BCA①若m 2020-12-25 …