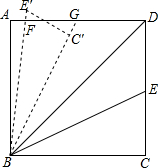
如图，在矩形ABCD中，AB=46，AD=10．连接BD，∠DBC的角平分线BE交DC于点E，现把△BCE绕点B逆时针旋转，记旋转后的△BCE为△BC′E′．当射线BE′和射线BC′都与线

Question

如图，在矩形ABCD中，AB=4 √(6)，AD=10．连接BD，∠DBC的角平分线BE交DC于点E，现把△BCE绕点B逆时针旋转，记旋转后的△BCE为△BC′E′．当射线BE′和射线BC′都与线段AD相交时，设交点分别为F，G．若△BFD为等腰三角形，则线段DG长为___．

Answer 1

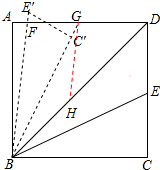在Rt△ABD中，由勾股定理，得
BD=√(AB2+AD2)=√((4√(6))2+102)=14，
在Rt△ABF中，由勾股定理，得：
BF²=（4√(6)）²+（10-BF）²，
解得BF=(49)/(5)，
AF=10-(49)/(5)=(1)/(5)．
过G作GH∥BF，交BD于H，
∴∠FBD=∠GHD，∠BGH=∠FBG，
∵FB=FD，
∴∠FBD=∠FDB，
∴∠FDB=∠GHD，
∴GH=GD，
∵∠FBG=∠EBC=(1)/(2)∠DBC=(1)/(2)∠ADB=(1)/(2)∠FBD，
又∵∠FBG=∠BGH，∠FBG=∠GBH，
∴BH=GH，
设DG=GH=BH=x，则FG=FD-GD=(49)/(5)-x，HD=14-x，
∵GH∥FB，
∴(FD)/(GD)=(BD)/(HD)，即((49)/(5))/(x)=(14)/(14-x)，
解得x=(98)/(17)．
故答案为：(98)/(17)．