早教吧作业答案频道 -->数学-->
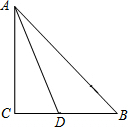
如图,在△ABC中,∠ACB=90°,AD平分∠CAB交BC于D,AC=6,BC=8,求S△ABD.
题目详情
如图,在△ABC中,∠ACB=90°,AD平分∠CAB交BC于D,AC=6,BC=8,求S△ABD.

▼优质解答
答案和解析
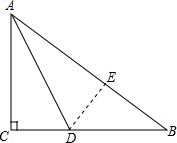 作DE⊥AB,垂足为E,DE即为D到AB的距离.
作DE⊥AB,垂足为E,DE即为D到AB的距离.
又∵∠C=90°,AD平分∠CAB,
∴DE=DC,
在△ABC中,∵∠C=90°,BC=8,AC=6,
∴AB=10,设CD=x,
则DE=CD=x,BD=8-x.
在Rt△ACD与Rt△AED中,∵
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,∴BE=4,
在Rt△BED中,∵DE2+EB2=DB2,即x2+42=(8-x)2,
解得:x=3,
∴S△ABD.=
AB•DE=
×10×3=15.
 作DE⊥AB,垂足为E,DE即为D到AB的距离.
作DE⊥AB,垂足为E,DE即为D到AB的距离.又∵∠C=90°,AD平分∠CAB,
∴DE=DC,
在△ABC中,∵∠C=90°,BC=8,AC=6,
∴AB=10,设CD=x,
则DE=CD=x,BD=8-x.
在Rt△ACD与Rt△AED中,∵
|
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,∴BE=4,
在Rt△BED中,∵DE2+EB2=DB2,即x2+42=(8-x)2,
解得:x=3,
∴S△ABD.=
| 1 |
| 2 |
| 1 |
| 2 |
看了如图,在△ABC中,∠ACB=...的网友还看了以下:
在等腰三角形ABC中AB=AC=5,BC=6,点E是BC边上的一点,ED垂直于AB交AB边于点D,E 2020-03-30 …
已知(a+b)/(ab)=6,(b+c)/(bc)=9,(a+c)/(ac)=15,求(abc)/ 2020-04-27 …
在直角三角形ABC中.角C等于90度,AC=8,CB=6,D是AB上任意一点,过点D作DE平行BC 2020-07-09 …
袋中有10个球,分别编有1到10,从中任取一球,设A={取得球的号码是偶数},B={取得球的号码是 2020-07-19 …
如图,在三角形ABC中,AB=AC=5,BC=6,D,E分别是边AB,AC上的两个动点(D不与AB 2020-07-22 …
(A类5分)如图1,平行四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E、F,求证:∠ADE 2020-07-30 …
乘法公式1.已知x,y,z都是正数,且x^3+y^2+z^2=3xyz,求证x=y=z2.若(a-b 2020-11-01 …
如图,三角形ABC中AB=AC=5,BC=6,矩形PQED的边PQ在线段BC上,DE分别在AB,AC 2020-11-07 …
,2如图,△ABC中,AB等于AC等于6,BC等于9,点P,D分别在边BC,AD上,联结AP,PD, 2020-12-07 …
平行四边形ABCD的周长32,5AB=3BC,则对角线AC的取值范围为()A.6<AC<10B.6< 2021-02-17 …