早教吧作业答案频道 -->物理-->
如图所示,半径为R的光滑圆环竖直固定,质量为3m的小球A套在圆环上;长为2R的刚性(既不伸长也不缩短)轻杆一端通过铰链与A连接,另一端通过铰链与滑块B连接;滑块B质量为m,套在水平
题目详情
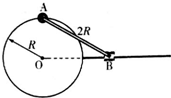
如图所示,半径为R的光滑圆环竖直固定,质量为3m的小球A套在圆环上;长为2R的刚性(既不伸长也不缩短)轻杆一端通过铰链与A连接,另一端通过铰链与滑块B连接;滑块B质量为m,套在水平固定的光滑杆上.水平杆与圆环的圆心O位于同一水平线上.现将A置于圆环的最高处并给A-微小扰动(初速度视为0),使A沿圆环顺时针自由下滑,不计一切摩擦,A、B均视为质点,重力加速度大小为g.求:
(1)A滑到与圆心O同高度时的速度大小;
(2)A下滑至杆与圆环第一次相切的过程中,杆对B做的功.

(1)A滑到与圆心O同高度时的速度大小;
(2)A下滑至杆与圆环第一次相切的过程中,杆对B做的功.
▼优质解答
答案和解析
(1)当A滑到与O同高度时,A的速度沿圆环切向向下,B的速度为0,由机械能守恒定律得: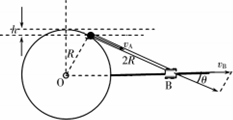
3mgR=
(3m)v2,
解得:v=
.
(2)杆与圆环相切时,A的速度沿杆方向,设为vA,此时B的速度设为vB,根据杆不可伸长和缩短,得:
vA=vBcosθ,
由几何关系得:cosθ=
,
球A下落的高度为:h=
R,
由机械能守恒定律得:3mgh=
(3m)vA2+
mvB2,
由动能定理得:W=
mvB2,
代入数据解得:W=
mgR.
答:(1)A滑到与圆心O同高度时的速度大小为
;
(2)A下滑至杆与圆环第一次相切的过程中,杆对B做的功为
mgR.

3mgR=
| 1 |
| 2 |
解得:v=
| 2gR |
(2)杆与圆环相切时,A的速度沿杆方向,设为vA,此时B的速度设为vB,根据杆不可伸长和缩短,得:
vA=vBcosθ,
由几何关系得:cosθ=
2
| ||
| 5 |
球A下落的高度为:h=
5-2
| ||
| 5 |
由机械能守恒定律得:3mgh=
| 1 |
| 2 |
| 1 |
| 2 |
由动能定理得:W=
| 1 |
| 2 |
代入数据解得:W=
15-6
| ||
| 17 |
答:(1)A滑到与圆心O同高度时的速度大小为
| 2gR |
(2)A下滑至杆与圆环第一次相切的过程中,杆对B做的功为
15-6
| ||
| 17 |
看了如图所示,半径为R的光滑圆环竖...的网友还看了以下:
给定椭圆C:,称圆心在原点O、半径为的圆是椭圆C的“伴椭圆”,若椭圆C的一个焦点为,其短轴上的一个 2020-06-18 …
(本题满分12分)给定椭圆:,称圆心在原点,半径为的圆是椭圆的“准圆”。若椭圆的一个焦点为,其短轴 2020-06-21 …
(2010•海淀区二模)给定椭圆C:x2a2+y2b2=1(a>b>0),称圆心在原点O,半径为a 2020-06-21 …
高中数学给定椭圆C:x²/a²+y²/b²=1(a>b>0),称圆心在原点O,半径为√(a²+b² 2020-06-30 …
给定椭圆C:+=1(a>b>0),称圆心在原点O,半径为的圆是椭圆C的“准圆”.若椭圆C的一个焦点 2020-07-04 …
给定椭圆:,称圆心在原点,半径为的圆是椭圆的“准圆”.若椭圆的一个焦点为,其短轴上的一个端点到的距 2020-07-30 …
为什么在确定的圆中,过圆内某一点的两条相互垂直的弦,当两弦为一个是直径和一个是最短弦时,两条弦长的 2020-07-31 …
(本小题满分15分)给定椭圆C:,称圆心在原点O、半径是的圆为椭圆C的“准圆”.已知椭圆C的一个焦点 2020-11-01 …
(本题满分14分)给定椭圆>>0,称圆心在原点,半径为的圆是椭圆的“伴随圆”.若椭圆的一个焦点为,其 2020-11-01 …
如图所示,半径为R的光滑圆环竖直固定,质量为3m的小球A套在圆环上;长为2R的刚性(既不伸长也不缩短 2020-11-02 …